В геометрической прогрессии b2=3 корень из 3, b3=9. Найдите S4.
Другие вопросы по теме Алгебра
Популярные вопросы
- Вкласi 12 хлопчикiв, що становить 3/8 усiх учнiв. скiльки всього учнiв в класi?...
2 - Сочинение на тему на кого я хочу быть похожим....
1 - Почему для добычи полезных ископаемых необходимо большое кол-во электроэнергии?...
3 - Cграфиков прямых y=7x+9 и y=1 получили, что эти прямые пересекаются в точке...
2 - Всхемах расставьте коэффициенты и укажите тип реакции: mno2 + c = co + mn koh...
1 - Какие средства выразительности используется в ходе славься?...
1 - Найдите первый член и знаменатель прогрессии, если b3 +b6 =140, b4 − b5 + b6...
1 - Среда обитания хищных динозавров(именно среда обитания: температура, влажность,...
1 - Какие признаки указывают на то, что моховидные растения древнее папоротниковидных?...
2 - На титрование навески н2с2о4×2н2o (масса 0,1139 г) затрачено 18,06 мл раствора...
3
Найдем знаменатель геометрической прогрессии:
Теперь найдём первый член заданной прогрессии:
Теперь найдём сумму первых четырёх членов заданной прогрессии:
ответ: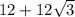 .
.