В двух ящиках содержится по 50 деталей, причём в первом — 16 стандартных деталей, а во втором — 18 стандартных деталей. Из второго ящика наудачу извлечена одна деталь и переложена в первый ящик. Определи вероятность того, что наудачу извлечённая деталь из первого ящика окажется стандартной.
ответ (укажи в виде сокращённой дроби):
P(A)=
.Группа туристов, в которой 6 мальчиков и 5 девочек, выбирает по жребию четырех дежурных. Какова вероятность того, что будет выбрано 2 мальчика и 2 девочки?
P=37
P=311
P=511
P=57
Другие вопросы по теме Алгебра
Популярные вопросы
- Наведіть власний приклад прислівника та спільнокореневого слова, як - шою частиною...
3 - Источник независимых сообщений имеет в алфавита 6 сообщений с вероятностями:...
3 - 1)В наш век уже никто не сомневается, что совсем скоро человек устремится к...
1 - В кастрюле нагревается 40л воды. 2,5 всей воды выкипает. Сколько л воды воды...
1 - У Саши было на 48 конфет больше, чем у Маши. Одновременно Саша и Маша отдали...
2 - Даны координаты векторов a(9;3) и в (-4;2). Найдите: A) координаты векторов...
1 - Сумма нескольких последовательных натуральных чисел равна 448. Найти все такие...
2 - Внаслідок взаємодії 1,125 кг метанової кислоти з етанолом, одержали 1,2 кг...
2 - В якому реченні є відокремлений додаток (розділові знаки вилучено) А Микола...
2 - Гральна кістка підкидається п разів. Знайти ймовірність того, що випаде 6:...
1
Вероятность того, что из второго ящика переложили в первый ящик стандартную деталь равна , то в первом ящике будет 51 деталей из них 19 стандартных. Вероятность того, что извлеченная деталь из первого ящика окажется стандартной равна
, то в первом ящике будет 51 деталей из них 19 стандартных. Вероятность того, что извлеченная деталь из первого ящика окажется стандартной равна 
Аналогично, из второго ящика не стандартную деталь переложить в первый ящик можно с вероятностью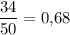 . Тогда в первом ящике будет 51 деталей из них 18 стандартных. Вероятность того, что из первого ящика выбранная деталь - стандартная, равна
. Тогда в первом ящике будет 51 деталей из них 18 стандартных. Вероятность того, что из первого ящика выбранная деталь - стандартная, равна 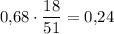
Искомая вероятность:
Вторая задача. Число всевозможных исходов равно числу выбрать 4 человек из 6+5=11, т.е.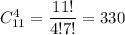 из них ищем благоприятные исходы: выбрать 2 мальчика и 2 девочки:
из них ищем благоприятные исходы: выбрать 2 мальчика и 2 девочки: 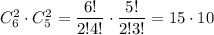
Искомая вероятность: