В арифметической прогрессии (а), в которой разность d + 0, сумма членов с седьмого по тринадцатый включительно равна 52,5. Найдите номер члена этой прогрессии, равного 7,5.
Другие вопросы по теме Алгебра
Популярные вопросы
- Визначте суму усіх натуральних чисел від 1 до 10...
2 - Тичяча шістсот пядесят пятому Який це розряд?...
3 - Скільки коренів має квадратне рівняння, якщо його дискримінант дорівнює:...
2 - сделать английский. Есть видео, но ответов незнаю https://www.liveworksheets.com/worksheets/en/English_as_a_Second_Language_(ESL)/Video_comprehension/Going_shopping_ar438210ug...
3 - У рівнобічній трапеції бічна сторона,висота і діагональ дорівнюють відповідно...
3 - Масса слона 5т а масса слоненка составляет 18% Найдите общую масссу...
2 - характеристика Софії з твору русалонька із 7-В або прокляття роду кулаківських....
1 - Кому і за що поклонялися давні слов яни? Пантеон слов янських богів...
2 - 13. Complete the sentences using one of the forms of used to Model 1...
2 - Доведіть що черепно-мозкові травми в підпотиличній ділянці є особливо...
2
Дано:
Найти:
Решение.
1)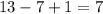 - количество членов с седьмого по тринадцатый.
- количество членов с седьмого по тринадцатый.
2)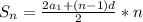 формула суммы
формула суммы 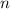 членов арифметической прогрессии
членов арифметической прогрессии
Для суммы членов с седьмого по тринадцатый первым
членом будет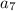 .
.
3) По формуле общего члена арифметической прогрессии
Подставим в уравнение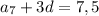 и получим:
и получим:
4) По условию один из членов данной прогрессии с номером
равен 7,5.
5) Очевидно, что два уравнения
имеют равные правые части 7,5 = 7,5 , а это значит, что
10-й член данной прогрессии равен 7,5.
ответ: 10.