уже 3й раз, никто не
(Все 6 уравнений)
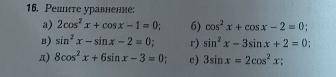
Другие вопросы по теме Алгебра
Популярные вопросы
- Вы с друзьями пошли в туристский поход в лес. Один из туристов получил травму...
2 - Составь короткие рассказы о ситуациях, в которые попали подростки с переломами...
1 - Каково значение личной гигиены для сохранения и укрепления здоровья?...
2 - Какие качества необходимо воспитывать в себе, чтобы повысить психологическую...
3 - В каких случаях необходимо вызывать «скорую...
1 - Как вы строите собственную систему здорового образа жизни?...
2 - Подготовьте небольшое сообщение на тему «Метод пальцевого прижатия артерий»....
1 - Напишите реферат на одну из тем: «Основные принципы противодействия терроризму...
1 - Что такое первая и кем она оказывается?...
2 - Подготовьте небольшое сообщение на тему «Влияние стресса на состояние здоровья...
3
замена:
n принадлежит Z.
корень t=2 не подходит , так как значения синуса входят только в [-1;1].
n принадлежит Z.
первый корень не подходит
n принадлежит Z.
второй корень не подходит
n принадлежит Z.
первый корень не подходит
n принадлежит Z.
второй не подходит
n принадлежит Z.