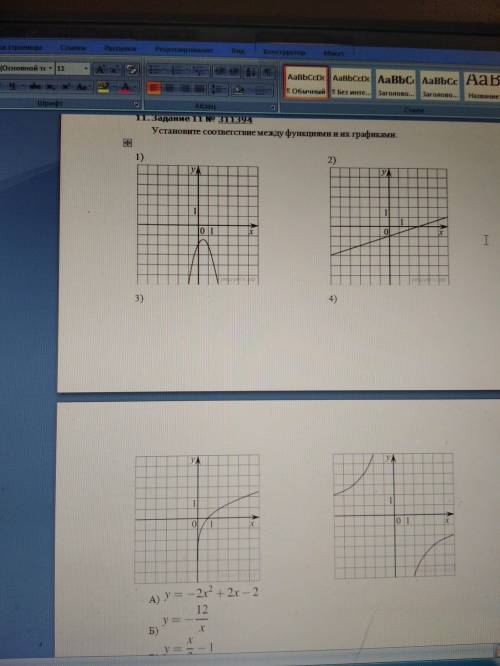
Утоновите соответствие между функциями и их графиком A) y=-2x²+2x-2
Б) y=-12/x
В) y=x/3-1

Добрый день, ученик! Давайте рассмотрим каждую функцию и постараемся сопоставить ее с соответствующим графиком.

A) Функция y = -2x² + 2x - 2.
Для начала, посмотрим на формулу функции. Мы видим, что коэффициент при x² отрицательный, это означает, что график функции будет направлен вниз. Также, есть коэффициенты перед x и свободный член (-2x и -2), которые будут влиять на положение графика. Чтобы изобразить данный график, я предлагаю рассмотреть несколько точек и построить его.

1) Подставим x = 0 в нашу функцию: y = -2(0)² + 2(0) - 2 = -2.
Таким образом, у нас есть точка (0, -2).

2) Подставим x = 1 в функцию: y = -2(1)² + 2(1) - 2 = -2 + 2 - 2 = -2.
Теперь у нас есть точка (1, -2).

3) Подставим x = -1 в функцию: y = -2(-1)² + 2(-1) - 2 = -2 + 2 - 2 = -2.
У нас есть точка (-1, -2).

Теперь, используя эти точки, мы можем построить график:

y
|
|
|
-1 |__________________
|
|
|
|
|
|_________________________ x

График функции A будет выглядеть как парабола, направленная вниз и проходящая через точки (0, -2), (1, -2) и (-1, -2).

B) Функция y = -12/x.
Рассмотрим формулу функции. Здесь нет переменной x в знаменателе, поэтому деление на ноль не возможно. Однако, обратите внимание, что коэффициент при x (-12) отрицательный, поэтому график будет направлен вниз.

1) Подставим x = 1 в функцию: y = -12/(1) = -12.
Имеем точку (1, -12).

2) Подставим x = -1 в функцию: y = -12/(-1) = 12.
У нас есть точка (-1, 12).

Теперь, используя эти точки, мы можем построить график:

y
|
|
|
-1 |_________________________
|
|
|
|
|
|_________________________ x

График функции B будет представлять гиперболу второго порядка, которая проходит через точки (1, -12) и (-1, 12).

C) Функция y = x/3 - 1.
Здесь у нас есть простая линейная функция, где коэффициент при x равен 1/3, что означает, что график будет наклонен вправо.

1) Подставим x = 0 в функцию: y = (0)/3 - 1 = -1.
Таким образом, у нас есть точка (0, -1).

2) Подставим x = 3 в функцию: y = (3)/3 - 1 = 1 - 1 = 0.
Имеем точку (3, 0).

3) Подставим x = -3 в функцию: y = (-3)/3 - 1 = -1 - 1 = -2.
У нас есть точка (-3, -2).

Теперь, используя эти точки, мы можем построить график:

y
|
x
|
-1 |_________________________
|
|
|
|
|
|_________________________ x

График функции C будет представлять прямую линию, которая проходит через точки (0, -1), (3, 0) и (-3, -2).

В итоге, мы сопоставили каждую функцию с ее соответствующим графиком.