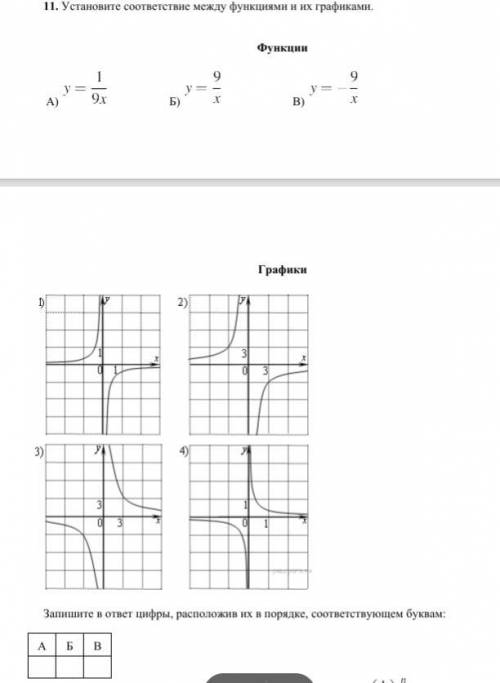
Установите соответствие между функциями и их графиками.
А)y=1/9x
Б)y=9/x
B)y=-9/x

Добрый день, уважаемый ученик!

Для установления соответствия между функциями и их графиками, мы должны проанализировать каждую функцию отдельно и сравнить ее с предложенными графиками. Давайте рассмотрим каждую функцию по очереди и проанализируем ее свойства, чтобы понять, как они соотносятся с графиками.

А) Функция y=1/9x:

Эта функция представляет собой прямую линию, проходящую через начало координат (0,0). Коэффициент при переменной x равен 1/9, что означает, что каждый раз, когда x увеличивается на 1, y увеличивается на 1/9. График этой функции будет представлять собой прямую линию, идущую вверх с наклоном вправо.

Б) Функция y=9/x:

Эта функция представляет собой гиперболу, определенную на всей числовой прямой за исключением точки x=0. При такой функции, чем больше значение x, тем меньше значение y и наоборот. График этой функции будет состоять из двух ветвей, направленных вниз и вверх, образуя гиперболу. График также будет симметричен относительно осям координат.

В) Функция y=-9/x:

Эта функция является другой гиперболой, определенной на всей числовой прямой за исключением точки x=0. В данном случае, при больших значениях x, значения y будут отрицательными и наоборот. График также будет состоять из двух ветвей, направленных вверх и вниз, образуя гиперболу. График будет симметричен относительно осям координат.

Теперь, когда мы проанализировали каждую функцию, давайте сопоставим их соответствующим графикам:

- Функция y=1/9x будет соответствовать графику A, так как она представляет собой прямую линию с положительным наклоном, проходящую через начало координат.

- Функция y=9/x будет соответствовать графику B, так как она представляет собой гиперболу с двумя ветвями, ориентированными вверх и вниз.

- Функция y=-9/x будет соответствовать графику C, так как она также представляет гиперболу с двумя ветвями, но ориентированными вверх и вниз, и значения y будут отрицательными.

Таким образом, мы установили соответствие между функциями и их графиками. При необходимости, вы всегда можете использовать экспоненциальный график для определения формы графика.