Установить, на какие линии плоскости w отображаются с функции w = 1 / z следующие линии плоскости z:
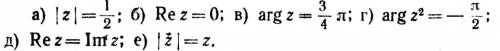
Популярные вопросы
- У меня завтра очень важная контрольная робота...
2 - (стр 11-16 литература 6 класс 2 часть Г.С.Меркин)...
3 - Які політичні сили найбільше вплинули на розвиток Франції на межі 19-20...
1 - Почему ребята ушли к партизанам от фашистов? Кто организовал ребятам школу...
3 - Содержание соли в поте можно измерить, определив молярную концентрацию...
2 - скільки грамім водяної пари міститься в 1 м³ повітря, якщо відносна вологість...
2 - Розглянь малюнки і встанови, якими коренями утворена коренева система запропонованих...
1 - Найдите область определения функции 1) y=2x+13 2) y= 2в числителе и 5x-11...
3 - сделайте по шагам решение полностью вас:)...
1 - Зробіть хронологічний ланцюжок створення антигітлерівської коаліції...
2
Давайте рассмотрим каждую линию плоскости z отдельно.
1) Прямая линия:
На исходной плоскости z прямая линия представляет собой множество точек, которые можно описать уравнением z = x + yi, где x и y - действительные числа.
Теперь применим функцию w = 1/z:
w = 1/(x + yi)
Для вычисления этого выражения, мы можем умножить числитель и знаменатель на сопряженное комплексное число z*, чтобы избавиться от мнимого знаменателя:
w = (1/(x + yi)) * (z*/z*)
w = z* / (|z|^2), где |z| - модуль числа z.
Таким образом, функция w = 1/z превращает прямую линию на плоскости z в окружность в плоскости w.
2) Вертикальная прямая:
Вертикальная прямая на плоскости z может быть представлена уравнением x = a, где a - действительное число.
Применяя функцию w = 1/z:
w = 1/(a + yi)
Мы можем снова умножить числитель и знаменатель на сопряженное комплексное число z*, чтобы избавиться от мнимого знаменателя. Получим:
w = (1/(a + yi)) * (z*/z*)
w = z* / (a^2 + y^2)
Функция w = 1/z превращает вертикальную прямую на плоскости z в гиперболу в плоскости w, которая открыта вдоль оси y.
3) Горизонтальная прямая:
Горизонтальная прямая на плоскости z может быть представлена уравнением y = b, где b - действительное число.
Применяя функцию w = 1/z:
w = 1/(x + bi)
Аналогично предыдущему примеру, умножим числитель и знаменатель на сопряженное комплексное число z*:
w = (1/(x + bi)) * (z*/z*)
w = z* / (x^2 + b^2)
Функция w = 1/z превращает горизонтальную прямую на плоскости z в гиперболу в плоскости w, которая открыта вдоль оси x.
Таким образом, функция w = 1/z отображает прямые линии на плоскости z в окружности, гиперболы или точки в плоскости w, в зависимости от исходной прямой линии.
Надеюсь, это ясно объясняет, как функция w = 1/z отображает линии плоскости z на линии плоскости w. Если у вас есть вопросы или что-то неясно, пожалуйста, сообщите мне, и я с радостью помогу!