Уровень В 1). М-середина AB. MB = 4 см, АК = 4 см, АС = 12 см. Найти Sвскм, если
SAMK = 4 CM².
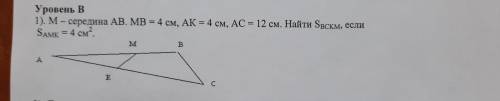
Другие вопросы по теме Алгебра
Популярные вопросы
- Найдите четвёртый член геометрической прогрессии (b)...
2 - Мальчик поднимал со дна колодца ведро,массой 18 кг,высота колодца составляет...
1 - Чем отличалось устройство Новгородской республики ( княжества) от других крупных...
2 - Составьте схему, запишите уравнения электродных процессов и рассчитайте ЭДС...
2 - ОТДАМ СТОЛЬНИК ТОМУ КТО РЕШИТ ВСЁ Некоторая материальная точка переместилась...
2 - Україна - багатонаціональна держава тому що?...
3 - Вспомни сказку и приведи свой пример, иллюстрирующий данный тип ресурсов -...
2 - Объясните смысл высказывания: «Кто не ищет дружбы с близким, тот себе заклятый...
3 - 1. Спишите, раскрывая скобки. . Волна б...ёт (НА) ВСТРЕЧУ текучей волне — быть...
2 - ФИЗКА 8 КЛАСС ФИЗКА 8 КЛАСС >...
1
На рисунке мы видим треугольник АBC.
Дано, что точка М является серединой отрезка AB, а также известно, что MB = 4 см, АК = 4 см и АС = 12 см.
Наша задача - найти площадь треугольника AMK, обозначенную как Sвскм.
Для решения этой задачи, мы можем воспользоваться знанием о свойстве медианы треугольника.
Медиана треугольника - это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Свойство медианы гласит, что медиана делит сторону треугольника, которую она пересекает, пополам.
Таким образом, мы знаем, что точка М является серединой отрезка АВ, а значит МК = МВ = 4 см.
Теперь мы можем построить отрезок СК и проверить его длину.
Для этого мы можем воспользоваться теоремой Пифагора для прямоугольного треугольника СМК, где СМ - высота треугольника, МК - половина основания, а СК - гипотенуза.
Теорема Пифагора гласит: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Согласно заданию, СМ = АС + АМ = 12 см + 4 см = 16 см.
Таким образом, у нас есть прямоугольный треугольник СМК, где СМ = 16 см, МК = 4 см и СК - искомая гипотенуза.
Применяя теорему Пифагора, мы можем найти длину СК.
16² = 4² + СК²
256 = 16 + СК²
СК² = 256 - 16
СК² = 240
СК = √240
СК = 4√15 см (по причине того, что корень из 240 можно упростить к виду 4√15)
Теперь у нас есть все необходимые данные для вычисления площади треугольника AMK.
Площадь треугольника можно найти, умножив половину произведения основания треугольника и его высоты.
Половина основания треугольника - это половина отрезка КМ, то есть половина от 4√15 см.
Высота треугольника - это отрезок СМ.
Теперь давайте найдем площадь треугольника AMK:
Sвскм = (1/2) * KK * СМ
Sвскм = (1/2) * 4√15 * 16
Sвскм = 32√15 см²
Таким образом, площадь треугольника AMK равна 32√15 см².