1. Алгебра
  2. Уравнение прямой которая

Уравнение прямой которая проходит через точку (1,-5) и перпендикулярна:

MissMi MissMi    1   30.09.2019 07:50    1

Ответы
Cuba125 Cuba125  09.10.2020 05:08

Задана прямая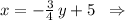  x=-\frac{3}{4}\, y+5\; \; \Rightarrow

\frac{3}{4}\, y= -x+5\; \; ,\; \; \; y=-\frac{4}{3}\, x+\frac{20}{3}

Угловой коэффициент прямой равен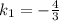  k_1=-\frac{4}{3} .  

Если прямые перпендикулярны, то их угловые коэффициенты удовлетворяют соотношению: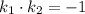   k_1\cdot k_2=-1  .

-\frac{4}{3}\cdot k_2=-1\; \; ,\; \; \; k_2=\frac{3}{4}

Уравнение прямой имеет вид: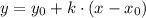  y=y_0+k\cdot (x-x_0) .

Точка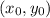  (x_0,y_0)  принадлежит прямой.

M(1,-5):\; \; \; y=-5+\frac{3}{4}\cdot (x-1)\\\\y=\frac{3}{4}\, x-\frac{23}{4}\\\\3x-4y-23=0

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
AdinaKhamzina1 AdinaKhamzina1  16.03.2021 11:13
Первое число равно х, а второе число в 14 раз больше первого. Если от второго числа отнять 56, а ко первому числу прибавить 48, то результаты будут равны. Найдите эти числа​...
emilligrin emilligrin  16.03.2021 11:13
Длина земельного участка прямоугольной формы на 10 м больше ширины, а его площадь равна 600-метровому квадрату. Длина и ширина земельного участка вычислить. ​...
orudcovamilana orudcovamilana  16.03.2021 11:13
с контрольной работой 8ласс...
Bonta Bonta  16.03.2021 11:12
Разложить на множители1.(a-b)³2.4x²-4xy+y2+10x-5y3.m²+n²+2mn+2m+2n+1 ​...
влаласт влаласт  16.03.2021 11:12
по графику функции определите а ) промежутки возрастания и убывания функции б ) промежутки звакопостянства функции...
Vova50915091 Vova50915091  28.08.2019 07:40
Разложите многочлен на множетели, представив один изтего членов в виде суммы подобныхтслагаемых: а)a2(степень)+8ab-9b2(степень) в)x2(степень)+4xy-12y2(степень)...
Jiio Jiio  28.08.2019 07:40
1)решите систему неравенств: {96*2^y+1 12 {16*4^y 1 2)найдите наименьшее целое значение решения системы неравенств: {4- y-1/3 =y {7y-1/8 6 3)найдите сумму корней уравнения:...
Snowandsand368 Snowandsand368  28.08.2019 07:40
Решить неравенство и найти наибольшое целое число, удовлетворяющее неравенству: 2(5x+1) 6,8+2x...
Denisigroman Denisigroman  28.08.2019 07:40
Решите неравенства: а)4x+7 11 б) 3y+1,3 (или равно)5y-0,1...
milena7772 milena7772  01.01.2020 12:09
Вклассе из 42 учеников, успеваемость урока иностранного языка среди девочек составила 75%,а среди мальчиков составила 40%.какова общая успеваемость учеников,если в классе...

Популярные вопросы