Уравнение касательной 1) [tex]y=rac{2}{x^{2} } -x[/tex] при [tex]x_{0} = -1[/tex]2) [tex]rac{3}{x^{2}

Question

Алгебра: Уравнение касательной 1) [tex]y=rac{2}{x^{2} } -x[/tex] при [tex]x_{0} = -1[/tex]2) [tex]rac{3}{x^{2} } +2x[/tex] при [tex]x_{0} = 1[/tex]

homeLoL · Answer

3 факта:- Уравнение касательной к графику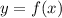 в точке 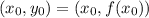:- Взятие производной - линейная операция: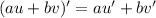 , a и и –  коэффициенты, u и v – дифференцируемые функции- Производная степени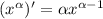 Используем:1) 2)...

Уравнение касательной 1) $y=\frac{2}{x^{2} } -x$ при $x_{0} = -1$
2) $\frac{3}{x^{2} } +2x$ при $x_{0} = 1$

Популярные вопросы

Уравнение касательной 1) при 2) при

Популярные вопросы

Уравнение касательной 1) $y=\frac{2}{x^{2} } -x$ при $x_{0} = -1$
2) $\frac{3}{x^{2} } +2x$ при $x_{0} = 1$