Упростите выражение (корень из 15 минус 1) умножить (в числители корень из 5 в знаминатиле корень из 3 минус корень из 5 минус в числители корень из 3 в знаминатиле корень из 5 плюс корень из 3)
Другие вопросы по теме Алгебра
Популярные вопросы
- Придумать гумореску с рифмами: -спросоння; попідвіконню-попідтинню....
3 - Как ответить на вопросы are we a big family. is he a good student. is he a swimmer....
1 - Решите уравнение : 2: (3/8х) = 1целая 4/9 : 4 целых 1/3...
1 - Нужно описание симона боливара по плану 1. внешность . 2.черты характера . 3.деятельность...
1 - Ученики делали гирлянды и игрушки. каждый мальчик сделал по 4 гирлянды и 3 игрушки,...
1 - Вдревнем китае впервые в научились 1) производить порох 2) играть в шахматы...
1 - Расположите в порядке возрастания дроби 5,72 5,8 5,075...
2 - Площадь квадрата 16 см² найдите ширину прямоугольника который имеет площадь...
3 - Запиши какое событие произошедшее во время правления петра 1 закрепило статус...
3 - Вримских библиотеках во всех книгах 12 букв ) это не вопрос а факт...
1
-14
Объяснение:
Условие задачи написано не корректно, то что вы написали можно по разному прочитать, но я всё же думаю, что вы имели в виду это:
(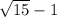 ) *
) * 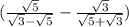 .
.
С первой скобкой ничего не поделаешь, но во второй скобке можно привести всё к общему знаменателю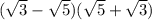 .
.
(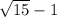 ) *
) * 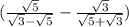 = (
= (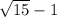 ) *
) * 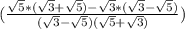 .
.
Далее во второй скобке раскрываем скобки в числители и знаменателе.
(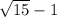 ) *
) * 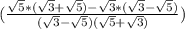 = (
= (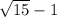 ) *
) * 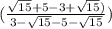 .
.
Во второй скобке после элементарных арифметических операций получаем:
(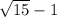 ) *
) * 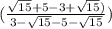 = (
= (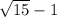 ) *
) * 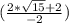 .
.
Во второй скобке сократим числитель и знаменатель на 2, получаем:
(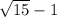 ) *
) * 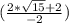 = (
= (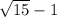 ) *
) * 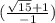 = (
= (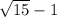 ) *
) * 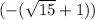 =
=
=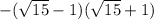 =
= 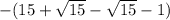 = -14.
= -14.