УПРОСТИТЕ ВЫРАЖЕНИЕ ДО ЧИСЛОВОГО ЗНАЧЕНИЧ
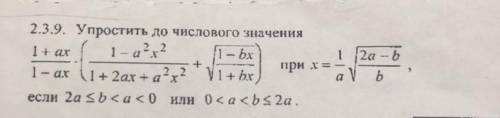
Другие вопросы по теме Алгебра
Популярные вопросы
- Напишите сочинение по обществоведению на тему роль личности в...
3 - Спишите, раскрывая скобки. укажите падеж собственных имен существительных....
3 - Два апельсина и пять мандаринов стоят столько же, сколько три апельсина...
2 - Основание равнобедренного треугольника равна 5 см , а боковая сторона...
2 - Турист проплыл по реке 90 км и пешком 10 км. при этом на пеший путь было...
2 - Наведіть приклади областей, території яких зазнавали певних змін. укажіть...
2 - 1. 2 в степени х+2 плюс 2 в степени х =5 2. 9 в степени х минус 6 умножить...
1 - 2)xквадрат+2х-4=0 решите уравнение))...
2 - Imagine you are going to have a birthday party. write a letter of invitation...
3 - Кто такие пингвины пингвины это-птицы,которые не умеют летать,пингвины...
3
ответ: 2
Объяснение:
(1+ax)/(1-ax) *( (1-a^2*x^2)/(1+2ax+a^2*x^2) +√( (1-b*x)/(1+b*x) ) )
Упростим:
(1-a^2*x^2)/(1+2ax+a^2*x^2) = (1-a*x)*(1+a*x)/(1+ax)^2 = (1-ax)/(1+ax)
(1+ax)/(1-ax) *( (1-ax)/(1+ax) + √( (1-b*x)/(1+b*x) ) ) =
= 1+ ( (1+ax)/(1-ax) ) * ( √( (1-b*x)/(1+b*x) ) )
x = 1/a * √( (2a-b)/b ) = 1/a * √( 2a/b -1)
a*x = √( 2a/b -1)
b*x =b/a * √( 2a/b -1)
Для удобства обозначим : √( 2a/b -1) = t, тогда
2a/b = t^2 +1
b/2a = 1/(t^2+1)
b/a = 2/(t^2+1)
a*x = t
b*x = 2t/(t^2+1)
1+b*x = 1+2t/(t^2+1) = (t^2+2t+1)/(t^2+1) = (t+1)^2/(t^2+1)
1-b*x = 1- 2t/(t^2+1) = (t^2-2t+1)/(t^2+1) = (t-1)^2/(t^2+1)
√( (1-b*x)/(1+b*x) ) =√( (t-1)^2/(t+1)^2 ) = |(t-1)|/|(t+1)|
1+ ( (1+ax)/(1-ax) ) * ( √( (1-b*x)/(1+b*x) ) ) = 1 +( (1+t)/(1-t) ) * |(t-1)|/|(t+1)|
Из условия : 2a<=b<a<0 или 0<a<b<=2a следует, что
1<=2a/b <2a/a = 2
0<=2a/b -1<1
0<= t < 1
-1<=t-1<0 → |(t-1)| = 1-t
1<=t+1 <2 → |t+1| = 1+t
Таким образом :
1 +( (1+t)/(1-t) ) * |(t-1)|/|(t+1)| = 1 + 1 = 2