Упростите выражение (-5)^n+1(-2)^n+¹(-1)^n+1/(-10)^n+1 -, где n- натуральное число.
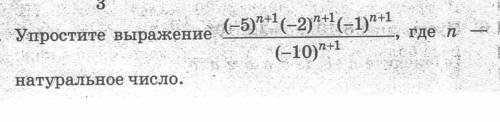
Другие вопросы по теме Алгебра
Популярные вопросы
- Найти производную функции y=sin^4x-cos(x^4)...
2 - Написать небольшое эссе по высказыванию учитесь у своего конкурента,потому...
2 - Match the words.write the sentences with these combinations of...
1 - Запиши выражение m3k15r39 в виде степени с показателем 3....
2 - С(показательная функция) 1)решить неравенство (0.5)в степени 6х...
1 - Длина самой маленькой акулы 50 см,а длина самого большого морского...
3 - Придумай сравнение-снег сияет,как ( ) снег лежит на деревьях как...
3 - Напишите отзыв на фильм карнавальная ночь...
2 - Разберите предложения по членам (определение, дополнение, обстоятельство):...
1 - Всостав воздуха входит 21% кислорода и 78% азота по объёму. рассчитайте...
3
A = (-5)^(n+1)
B = (-2)^n+1
C = (-1)^(n+1)
D = (-10)^(n+1)
Теперь у нас есть 4 переменные, и мы можем упростить каждую из них по отдельности.
Для переменной A, мы знаем, что отрицательное число в степени с нечетным показателем всегда будет отрицательным числом, а с четным показателем - положительным числом. Так как (n+1) всегда будет четным числом (так как n - натуральное число), то A будет всегда положительным:
A = (-5)^(n+1) = 5^(n+1)
Для переменной B, мы знаем, что умножение двух отрицательных чисел дает положительное число. Так как (-2) в степени с четным показателем всегда будет положительным (так как n+1 - нечетное число), то B будет всегда положительным:
B = (-2)^n+1 = 2^(n+1)
Для переменной C, мы знаем, что (-1) в любой степени является чередующейся последовательностью, то есть чередует знаки "+" и "-". Так как (n+1) всегда будет нечетным числом, то C будет всегда отрицательным:
C = (-1)^(n+1) = -1
Для переменной D, мы знаем, что (-10) в степени с четным показателем всегда будет положительным, а с нечетным показателем - отрицательным. Так как (n+1) всегда будет нечетным числом (так как n - натуральное число), то D будет всегда отрицательным:
D = (-10)^(n+1) = -10^(n+1)
Теперь, объединяя все наши результаты, получаем:
(-5)^(n+1) (-2)^n+1 (-1)^(n+1) / (-10)^(n+1) = 5^(n+1) * 2^(n+1) * -1 / -10^(n+1)
При умножении степеней одного и того же числа, мы складываем их показатели. Таким образом, получаем:
= 5^n * 5 * 2^n * 2 * -1 / -10^n * -10
= -10 * 5^n * 2 * 2^n / -10^n * -10
При делении степеней одного и того же числа, мы вычитаем их показатели. Таким образом, получаем:
= -10 * 5^n * 2 * 2^n / -10^n * -10
= (5^n * 2^(n+1)) / (-10^n * -10)
= 5^n * 2^(n+1) / 10^n * 10
Теперь мы можем упростить это выражение путем сокращения:
= (5^n * 2 * 2^n) / (10 * 10^n)
= (2 * 5^n * 2^n) / (10 * 10^n)
= 2^(n+1) * 5^n / 10^(n+1)
= 2 * 5^n / 10
= 2 * (5^n / 10)
= 2 * (1/2) * 5^n
= 5^n
Таким образом, упрощенное выражение будет равно 5 в степени n. Ответом на данный вопрос будет 5^n.