Упростить выражение при a>0,b>0: А) (a^(-3) ∛(a^6 b^2 ))/∛b
Б)(1/a^(√(2 )-1 ) )^(√2+1)∙a^(√2+1)
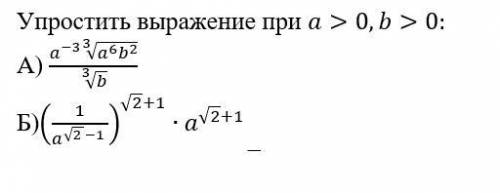
Другие вопросы по теме Алгебра
Популярные вопросы
- 1) тревожиться за исход сражения; 2) уверенность в победу российских...
2 - Составить текст мой дом с переводом...
1 - Ввести с клавиатуры символ-маленькую букву. напечатать соответствующую...
3 - Одноклеточная амёба каждые 3 часа делится на 2 части. определить сколько...
3 - Втреугольнике точка м - середина стороны вс. параллелограмм всде построен...
2 - Докажите равенство (5−2√6)÷(5+2√6)=49−20√6...
3 - На шелковой нити в воздухе висит неподвижно шарик массой 4 г, имеющий...
1 - Правда ли, что ядро планеты земли состоит из железа и никеля?...
3 - Составте план о бородино со словами из текста...
2 - Отметьте основные черты развития южных штатов сша. 1. развитие крупного...
3
А) Для начала упростим числитель выражения (a^(-3) ∛(a^6 b^2 )).
Используем свойство a^m ∙ a^n = a^(m+n), чтобы умножить степени a:
(a^(-3) ∛(a^6 b^2 )) = a^(-3) ∙ a^(6/3) ∙ b^(2/3)
Здесь a^(-3) - это обратное значение a^3, a^(6/3) = a^2, а b^(2/3) - это кубический корень из b^2.
Теперь, чтобы упростить этот результат, используем еще одно свойство: кубический корень из a^b равен a^(b/3):
a^(-3) ∙ a^(6/3) ∙ b^(2/3) = a^(-3) ∙ a^2 ∙ b^(2/3) = a^(-3 + 2) ∙ b^(2/3) = a^(-1) ∙ b^(2/3) = (1/a) ∙ b^(2/3)
Теперь перейдем к знаменателю выражения - ∛b. Заметим, что кубный корень из b может быть записан как b^(1/3).
Таким образом, упрощенное выражение будет:
( (1/a) ∙ b^(2/3) ) / (b^(1/3)) = (1/a) ∙ b^(2/3 - 1/3) = (1/a) ∙ b^((2-1)/3) = (1/a) ∙ b^(1/3) = (1/a) ∙ ∛b
Ответ: (1/a) ∙ ∛b.
Б) Для начала посмотрим на выражение в скобках: (1/a^(√(2 )-1 ) )^(√2+1)∙a^(√2+1).
Обратим внимание, что a^(√2+1) - это произведение a^√2 и a^1.
Также заметим, что (1/a^(√(2 )-1 ) )^(√2+1) - это произведение (1/a^(√(2 )-1 ) ) и (1/a^(-√(2 )-1 ) ).
Теперь упростим выражение:
(1/a^(√(2 )-1 ) )^(√2+1)∙a^(√2+1) = (1/a^√2 ) ∙ (1/a) ∙ a^√2 ∙ a
Заметим, что a^√2 и 1/a^√2 взаимно обратны. Это означает, что их произведение равно 1.
Таким образом, упрощенное выражение будет:
(1/a) ∙ a = 1.
Ответ: 1.
Я надеюсь, что мое объяснение помогло вам понять, как упростить данные выражения. Если у вас возникнут еще вопросы, не стесняйтесь задавать.