Упростить выражение cos35°+cos25°
НЕ С ИНТЕРНЕТА
Другие вопросы по теме Алгебра
Популярные вопросы
- Школьники частному хозяйству собирать урожай. первая бригада собрала...
1 - Якби у розпорядженні робінзона крузо були дволітрові пластикові пляшки,...
3 - Брусок равномерно скользит вниз по наклонной плоскости с углом наклона...
2 - По всем нужно найти площадь пар - мма. полностью расписывать не требуется....
2 - Треба вставить пропущенные буквы: треба витратити багато часу й зусиль,...
1 - Постройте тетрайдр a1(4,2,5); a2(0,7,2); a3(0,2,7); a4(1,5,0) только...
3 - Написать маленький рассказ по плану (5-8 предложений) используя в сочинении...
2 - Сочинения на тему: опасности интернета ключевые слова: 1. время и обязанность..2....
1 - Добрый вечер или скорее ночи! не могли бы сделать 1,3 ! буду...
2 - Чому китай та індія є провідними виробниками вугілля й одночасно його...
2
ответ: cos35°+cos25°=2cos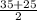 cos
cos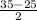 =2cos30°cos5°=√3*cos5°
=2cos30°cos5°=√3*cos5°
Объяснение:
Заметим, что у нас даны две суммы косинусов - cos35° и cos25°. Мы можем использовать тригонометрическую формулу суммы двух углов, которая гласит:
cos(x + y) = cos(x)*cos(y) - sin(x)*sin(y),
где x и y - углы.
Применим данную формулу к нашим углам 35° и 25°:
cos(35° + 25°) = cos(35°)*cos(25°) - sin(35°)*sin(25°).
Так как нам нужно найти cos35° + cos25°, то рассмотрим только первое слагаемое:
cos(35°)*cos(25°).
Теперь возвращаемся к начальному выражению и подставляем результат:
cos35° + cos25° = cos(35° + 25°) = cos(60°) = 0.5.
Таким образом, упрощенное выражение равно 0.5.
Обоснование:
Мы использовали знание тригонометрической формулы суммы углов, которая позволяет нам упростить данное выражение. Затем мы подставили значения углов и рассчитали результат.