Упростить выражение.
((cos2b-cos6b)/(sin6b-sin2b))+tg2b
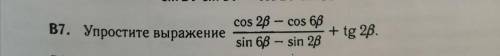
Другие вопросы по теме Алгебра
Популярные вопросы
- Если не сложно)реакция получения бромида магния, если я рассматриваю такой...
3 - Как найти объём правильной шестиугольной призмы если известны основания...
3 - По 1. объем тела (размеры в мм)2. выталкивающая сила...
1 - Скласти речення з поданими словами ставляючи їх у родовому відмінку однини...
1 - ответить на вопросы на языке нужно заранее...
1 - Втечение 30 с поезд двигался равномерно со скоростью 72км/ч. какой путь...
2 - Чем объяснить противоречивые впетчатления о деде алёши?чем выгодно отличает...
3 - Вопросы по произведению евгений онегин. 1-осознаёт ли татьяна последствия...
3 - Решить примеры! пишу такой пример: 2(а+5)...
3 - Диалог у публицыстычному стыли.....
2
решение смотри на фотографии
Формулы: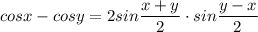 ,
,