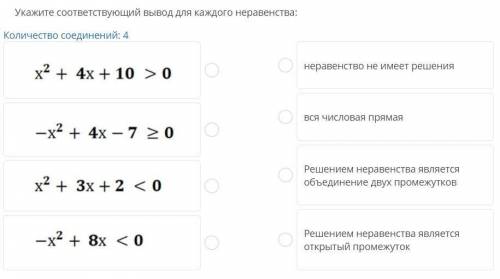
Укажите соответствующий вывод для каждого неравенства: Количество соединений: 4
x2 + 4x+ 10 > 0
неравенство не имеет решения
вся числовая прямая
-x2 + 4x - 7 > 0
x2 + 3x + 2 < 0
Решением неравенства является
объединение двух промежутков
-x2 + 8x < 0
Решением неравенства является
открытый промежуток

Объяснение:

1) x² + 4x+ 10 > 0

  x² + 4x+4-4+ 10 > 0

(x+2)²+6> 0- вся числовая прямая

x² + 4x+ 10 > 0 - вся числовая прямая

2) -x² + 4x - 7 > 0⇔x²-4x+7<0⇔(x²-4x+4-4+7<0⇔(x-2)²+3<0

Так (x-2)²+3>0 при ∀х, то

-x² + 4x - 7 > 0 - неравенство не имеет решения

3) x² + 3x + 2 <  0  x²+2·х·1,5+2,25- 2,25+2<0⇔(x+1,5)²-0,25<0⇔(x+1,5)²-0,5²<0⇔(x+1)(x+2)<0 ⇒x∈(-2;-1)

x² + 3x + 2 <  0 - Решением неравенства является

открытый промежуток

4) -x² + 8x < 0⇔x²-8x>0⇔x(x-8)>0

  решением является: х∈(-∞;0)∪(8;+∞)

-x² + 8x < 0  - Решением неравенства является

объединение двух промежутков