Укажите наибольшее значение выражения 2х-4у-х^2-у
Другие вопросы по теме Алгебра
Популярные вопросы
- решить пример. Если в некоторой десятичной дроби перенести запятую...
2 - На рисунке большой круг показывает множество всех учеников класса....
2 - Складчатые горы — это . горы, сформированные в результате разрывов...
1 - Решите задачу Велосипедист за 3 ч проехал 50,4 км затем его скорость...
1 - Найдите длину ломаной, если 5/2 ее длины равны 24 см. ответ укажите...
2 - Я знал красавиц недоступных, холодных, чистых как зима. ОБЪЯСНИТЕ...
3 - 4 класс Украинский язык страница 40 упражнения 82...
3 - Для чего нужно бережное отношение к традиции?...
2 - Определить соматических и половые клетки по рисункам...
1 - Жерде алыстан бакылайды.стансыларга турле суреттер жебереды,...
1
ответ: 5 .
Так как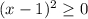 и
и 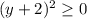 , то наименьшее значение, которое принимают эти выражения равно 0 . Значит наибольшее значение , которое принимает выражение
, то наименьшее значение, которое принимают эти выражения равно 0 . Значит наибольшее значение , которое принимает выражение  равно 5-0-0=5 .
равно 5-0-0=5 .