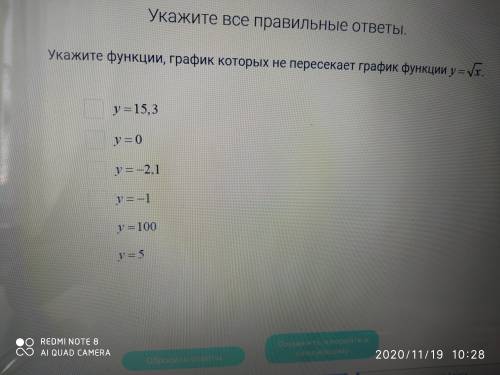
Укажите функции, график которых не пересекает график функции y=√x

Для того чтобы определить функции, графики которых не пересекают график функции y=√x, нам нужно найти уравнения этих функций и проверить их на пересечение с графиком y=√x.

Для начала, давайте рассмотрим график функции y=√x. График этой функции представляет собой положительную половину параболы с вершиной в точке (0,0), которая стремится к бесконечности при увеличении значения x. График y=√x проходит через все точки с положительными значениями x и y.

Теперь мы должны найти функции, графики которых не пересекают график y=√x. Для этого мы можем использовать неравенства.

Предположим, у нас есть функция f(x), график которой не пересекает график y=√x. Это означает, что для любого значения x, функция f(x) должна быть либо выше, либо ниже этого графика.

Давайте рассмотрим несколько примеров функций, которые могут удовлетворять этому условию:

1. Функция y=3: График этой функции является горизонтальной линией на уровне y=3. Он символизирует то, что функция f(x) всегда возвращает значение 3, независимо от значения x. График функции y=3 не пересекает график y=√x, так как для любого значения x, √x всегда будет больше или равно 0.

2. Функция y=-2: График этой функции тоже является горизонтальной линией, но на уровне y=-2. Он символизирует то, что функция f(x) всегда возвращает значение -2, независимо от значения x. График функции y=-2 также не пересекает график y=√x, так как √x всегда будет больше или равно 0.

Оба этих примера являются решениями задачи, и графики этих функций не пересекают график y=√x.

В обоих случаях доказательство того, что графики функций не пересекаются с графиком y=√x, основывается на знании особенностей графика функции y=√x. Поскольку y=√x всегда больше либо равна 0, функции, которые всегда возвращают отрицательные или постоянные значения, не пересекут этот график.