Укажи члены последовательности (an) которые расположены между: a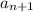tex]a_{n-3}[/tex] и

Для того чтобы найти члены последовательности (an), которые расположены между a_{n+1} и a_{n-3}, нам нужно разобраться в формулах, которые определяют каждый из членов последовательности.

Для начала, давайте разберемся, что означают a_{n+1} и a_{n-3}.

a_{n+1} обозначает член последовательности, который следует прямо за членом a_n.
a_{n-3} обозначает член последовательности, который находится на три позиции до члена a_n.

Используя эти определения, мы можем уточнить, что мы ищем члены последовательности, которые следуют прямо за членом, который находится на три позиции до a_n.

Теперь обратимся к формуле, которая определяет каждый член последовательности. Пусть формула имеет вид:

a_n = f(n)

где f(n) - это функция, которая связывает каждое число n с соответствующим членом последовательности a_n.

Для того чтобы найти члены последовательности, которые нас интересуют, мы можем использовать два метода:

1. Метод подстановки: Подставляем значения n+1 и n-3 вместе с n в формулу a_n = f(n) и находим значения a_{n+1} и a_{n-3}. Затем находим все члены последовательности между a_{n+1} и a_{n-3}, если они существуют.

2. Метод решения уравнения: Создаем уравнение, в котором положим a_{n+1} = a_{n-3}, и решаем его относительно n. Затем, используя полученные значения n, находим все члены последовательности между a_{n+1} и a_{n-3}, если они существуют.

Оба метода могут быть использованы для нахождения членов последовательности, которые нас интересуют. Выбор метода будет зависеть от конкретной формулы, которая определяет последовательность в вашем задании.

Например, если формула последовательности a_n = 2n + 1, то мы можем использовать метод подстановки:

1. Подставляем значения n+1 и n-3 вместе с n в формулу:
a_{n+1} = 2(n+1) + 1 = 2n + 2 + 1 = 2n + 3
a_{n-3} = 2(n-3) + 1 = 2n - 6 + 1 = 2n - 5

2. Находим все члены последовательности между a_{n+1} и a_{n-3}:
a_{n+1} = 2n + 3
a_n = 2n + 1
a_{n-1} = 2n - 1
a_{n-2} = 2n - 3
a_{n-3} = 2n - 5

В данном примере, все члены последовательности между a_{n+1} и a_{n-3} будут:
a_n, a_{n-1}, a_{n-2}, a_{n-3}

Надеюсь, что это объяснение и решение помогло вам понять, как найти члены последовательности, которые находятся между a_{n+1} и a_{n-3}. Если у вас есть еще вопросы или нужна дополнительная помощь, пожалуйста, сообщите.