Укажіть найбільше ціле значення параметра a при якому не має розвязків нерівність x^2-|2x-1| < a
Другие вопросы по теме Алгебра
Популярные вопросы
- Определить средне годовую температуру январь -19° февраль -11° март -2° апрель +3°...
3 - Втрудовом кодексерф, записано что трудовой договор с работниками может быть расторгнут...
2 - Синтаксический разбор предложения кажется шепчут колосья друг другу...
3 - Какую тему можно выбрать для полит информации в 8 классе. предложите хотя-бы три...
1 - Семья посадила 20 кг кортофеля, а собрала в 4 раза больше. сколько килограммов кортофеля...
3 - :решить уровнение (5-х)в квадрате -х(2,5+х)=0...
2 - Найдите значение выражения -27+68-56+61...
2 - Запиши все двузначные числа ,в разряде десятков которых есть цифра1...
1 - Кто написал басню лебедь рак и щука?...
3 - Вычислите в)3/24-5/18; г)7/24+11/18....
1
Построим график функции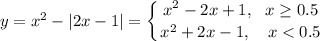
Если подставим a = -2, то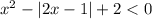
Если x ≥ 0.5, то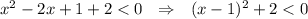
Это неравенство не выполняется для x ∈ [0.5;+∞).
Если x < 0.5, то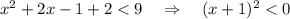
Это неравенство тоже неверно.
При y≤-2, т.е. при a≤-2 неравенство решений не имеет. Откуда наибольшее целое значение параметра: a = -2.