Указать самое большое целое значение параметра а, при котором вышеуказанное уравнение имеет два различных корня

Question

Алгебра: Указать самое большое целое значение параметра а, при котором вышеуказанное уравнение имеет два различных корня

Kykyblohka · Answer

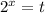Пусть 2^x=t при этом 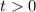, получим квадратное уравнение

$t^2+(a+1)t+\dfrac{1}{4}=0\\ \\ D=(a+1)^2-4\cdot \dfrac{1}{4}=(a+1)^2-1=(a+1-1)(a+1+1)=a(a+2)0\\ \\ a \in (-\infty;-2)\cup (0;+\infty).$

Далее для того чтобы исходное уравнение имело два различных корня, необходимо чтобы корни уравнения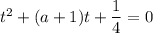 $t^2+(a+1)t+\dfrac{1}{4}=0$ были положительными. По теореме Виета:

$t_1+t_2=-(a+1)0~~~~\Rightarrow~~~a 0$

С учетом существования корней, получим что при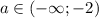 $a \in (-\infty;-2)$ данное уравнение имеет два различных корня, откуда наибольшее целое значение параметра a = -3

ответ: a = -3.

Указать самое большое целое значение параметра а, при котором вышеуказанное уравнение имеет два различных корня

Популярные вопросы