1. Алгебра
  2. Углубленная алгебра. Малая

Углубленная алгебра. Малая теорема Ферма, кратность. Доказать, что (4³⁶ - 1) ⋮ 323
Подсказка: 323 = 19 * 17

Alieta Alieta    2   06.03.2021 21:09    0

Ответы
vikatisenko1 vikatisenko1  05.04.2021 21:10

ответ: в описании

Объяснение:

323=19*17;

4^{36} -1=(4^{18} -1)(4^{18}+1);

По малой т. Ферма: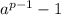 a^{p-1} -1 делится на p, если р - простое число и a - целое число, не делящиеся на р. В нашем случае, р=19 (простое число) , а=4 (не делится на 19):

4^{18} -1=4^{19-1} -1, значит, 4^{18} -1 делится на 19.

Осталось доказать, что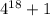 4^{18} +1 делится на 17.

Замечаем, что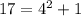 17=4^{2} +1. Делим многочлен на многочлен:

\frac{4^{18} +1}{4^{2}+1 } =4^{16}-4^{14}+4^{12}-4^{10}+4^{8}-4^{6}+4^{4}-4^{2}+1

\\Делил уголком\\

Так как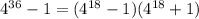 4^{36} -1=(4^{18} -1)(4^{18}+1) делится на 19 и на 17, то оно делится

и на 323

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
vdimitrievap0donn vdimitrievap0donn  11.06.2019 11:10
Найти область определения функции у=√х−9...
6hh6h6h 6hh6h6h  11.06.2019 11:10
На какую цифру оканчивается сумма чисел 3 в 2005 степени + 4 в 2006 степени?...
markzastawa markzastawa  11.06.2019 11:10
Сократите дробь: m^2-n^2 2m^2+4mn+2n^2...
Hiccjhcvkjxg Hiccjhcvkjxg  11.06.2019 11:10
Измерте рост двенадцати солдат в см подразделения , получили следущие данные , найдите средний рост солдата подрапзделения и число солдат выше среднего роста...
sPHAgNUM1 sPHAgNUM1  11.06.2019 11:10
Мастеру необходимо обтянуть тканью стулья. сиденье стула имеет форму квадрата со стороной 40 см. для того чтобы обтянуть сиденье, необходим целый кусок ткани с запасом по 15 см с...
DEN23567893 DEN23567893  09.08.2019 11:10
Студентка спешит попасть на электричку ,чтобы успеть на первую пару.до отхода поезда остается две минуты,а путь до вокзала 2 км.если первый километр она будет со скоростью 15км/ч,то...
Kolyakek Kolyakek  09.08.2019 11:10
Тригонометрические выражения. 1.sina/1+cosa-sina/1-cosa 2.1+tg^2a...
kallor12 kallor12  09.08.2019 11:10
Решить : длина земельного участка прямоугольной формы в 5 раз больше его ширины. если увеличить ширину на 9 м, то ее площадь увеличится в 4 раза. найдите первоначальные размеры этого...
Ganshit Ganshit  09.08.2019 11:10
Решите уравнение (3,2х-1,,2х+3,4)=-5,8...
tutuginovvan tutuginovvan  09.08.2019 11:10
Между какими целыми числами находится число корень23...

Популярные вопросы