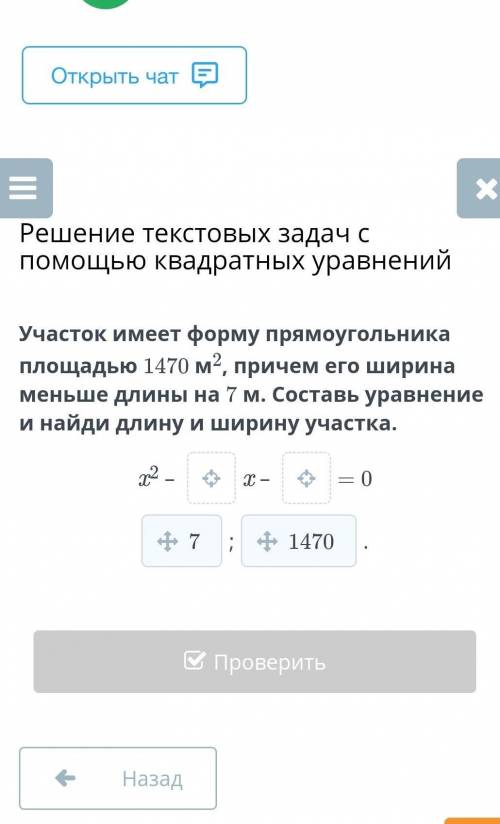
Участок имеет форму прямоугольника площадью 1470 м2, причем его ширина меньше длины на 7 м. Составь уравнение и найди длину и ширину участка. x2 – 

x – 

= 0

​

x2 - 7 х - 1470 = 0.

Объяснение:

Для решения данной задачи нам необходимо составить уравнение по условию задачи и решить его.

Дано, что площадь участка равна 1470 м2 и его ширина меньше длины на 7 м. Обозначим ширину участка как х (в метрах), а длину участка как х + 7 (в метрах).

Таким образом, мы имеем следующую систему уравнений:

1. Площадь участка равна 1470 м2:
х * (х + 7) = 1470

2. Ширина участка меньше длины на 7 м:
х + 7 < х

Теперь решим систему уравнений по порядку:

1. Распишем уравнение для площади участка:
х * (х + 7) = 1470

Раскроем скобки:
х^2 + 7х = 1470

Перенесем все члены в левую часть уравнения:
х^2 + 7х - 1470 = 0

2. Теперь решим полученное квадратное уравнение.

Мы получили квадратное уравнение вида ax^2 + bx + c = 0, где a = 1, b = 7 и c = -1470. Для его решения использовать формулу дискриминанта:

D = b^2 - 4ac
D = 7^2 - 4 * 1 * (-1470)
D = 49 + 5880
D = 5929

Теперь найдем корни уравнения, используя формулу:
x = (-b ± √D) / (2a)

x1 = (-7 + √5929) / (2 * 1) = (-7 + 77) / 2 = 70 / 2 = 35
x2 = (-7 - √5929) / (2 * 1) = (-7 - 77) / 2 = -84 / 2 = -42

Теперь проверим, какое из найденных значений подходит по условию задачи. Мы знаем, что ширина участка должна быть меньше длины на 7 м:
x + 7 > x

Подставим значения x1 и x2 в это неравенство:

Для x1: 35 + 7 = 42, что больше 35 - неравенство неверное.
Для x2: -42 + 7 = -35, что меньше -42 - неравенство верное.

Таким образом, получаем, что x2 = -42 не подходит под условия задачи.

Итак, длина участка будет равна x1 = 35 м, а ширина участка будет равна x2 = -35 м (в данном случае значение не имеет, так как не отвечает условию задачи).

Ответ: Длина участка - 35 м, ширина участка не определена.