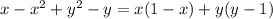у выражение
а) (6а-3)(а+1) - 3а(2а-3)
б)36x (x+2)-(6x+1) в квадрате
в) (4с-3) в квадрате -(2с-7)(7+2с)
2.разложите на множители
а) 36x-x в девятой степени
б) 5x в квадрате -20xy+20x в квадрате
3.у выражение
а) 4(2b-b в квадрате) в квадрате - b в квадрате (2b-1)(1+2b)+b в квадрате (16b-1)
4.разложите на множители
а (в 4 степени) - 1/16
б)x-x(в квадрате)+y(в квадрате)-y
Заранее
Другие вопросы по теме Алгебра
Популярные вопросы
- Выразите значения выражения lg 300 через m, если m = lg 3...
2 - (3ч.32мин.-1ч.48мин.+5ч.56мин.): 23*72...
3 - Дана молекула днк с относительной молекулярной массой 69 000, из них 8625 приходится...
3 - Поставь знаки действий и скобки между цифрами так, чтобы равенства стали верным...
1 - Какая правовая семья может быть охарактеризована следующими словами: судьи творят...
2 - Примеры существовавших в разных странах молодежных организаций: а)возникших стихийно...
1 - Определив, по какому признаку объединены слова, вычеркните «лишнее» слово. 1) тиски,...
1 - Хвостики! the british are considered to have a strong sense of humour,? you have...
1 - Найдите угол между прямыми ав и сд, если а (3,-1,3), в (3,-2,2), с (2,2,3), и д...
3 - Решить уравнение: 6,8*l5х-24l+2,3=4 * - умножить ll - модуль...
3
Объяснение:
1. Поэтапно раскрываем скобки
1а) (6а-3)(а+1)-3а(2а-3)=(6а-3)(а+1)-3а*2а-3а*(-3)=(6а-3)(а+1)-6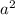 +9a=6a*a-3a+6a-3-6
+9a=6a*a-3a+6a-3-6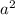 +9a=12а-3
+9a=12а-3
1б)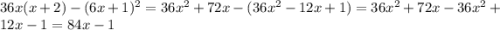
1в)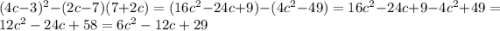
2а)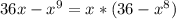
2б)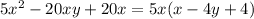
3)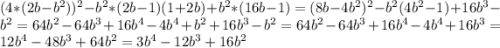
4а)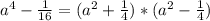
4б)