У тригонометрическое выражение:
8tg945° + tg(810°+a) - ctg(450°-a)

8 – 1 / (sin(a)*cos(a))

Объяснение:

Враховуємо, що період тригонометричних функції tg і ctg рівний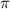 , а потім використовуємо формули зведення.

8tg945° + tg(810°+a) - ctg(450°-a) =  

= 8tg(900°+45°) + tg(720°+90°+a) - ctg(360°+90°-a) =

= 8tg45° + tg(90°+a) - ctg(90°-a) = 8*1 + (- ctg(a)) - tg(a) =

= 8 – cos(a)/sin(a) – sin(a)/cos(a) = 8 – ((cos(a))^2 +sin(a))^2)/ (sin(a)*cos(a)) =

= 8 – 1 / (sin(a)*cos(a))