У числа 209! вычислили сумму цифр. у полученного числа опять вычислили сумму цифр. и так продолжали до тех пор, пока не получили однозначное число. что это было за число? (109!=1*2*3*4*...*109)
​

9

Объяснение:

Заметим, что сумма цифр у числа будет иметь такой же остаток по модулю 9, что и само число, так как пусть число имеет вид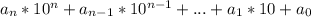 заметим, что число вида 10^n-1 делится на 9, так как оно будет состоять из одних девяток, значит число вида 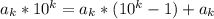сравнимо с 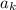по модулю 9. Значит все число сравнимо с суммой цифрой по модулю 9. Так как 209! делится на 9 (содержит множитель 9), то сумма цифр будет делится на 9 ⇒ сумма суммы цифр делится на 9 и. т.д. Таким образом, однозначное число будет делится на 9, значит оно равно 0 или 9, но равно 0 оно быть не может, так как сумма цифр у натурального числа ненулевая, так как содержит хотя бы 1 не 0. Значит она равна 9