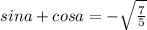Тригонометрия, 11 класс. С решением
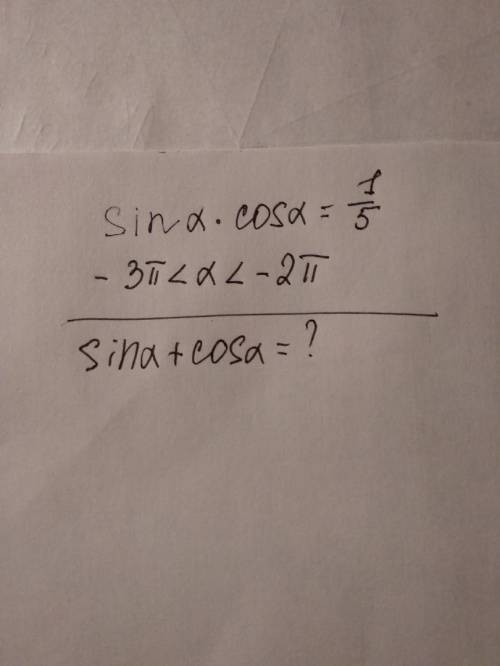
Другие вопросы по теме Алгебра
Популярные вопросы
- Хлопчик затиснув у руці мідну монету масою 5г за темпера-тури 16,6...
1 - Вычислите приближенно а + в, если а = 12,537 в = 6,(28), округлив...
2 - 4. Радиус окружности равен 6 см. Найдите длину этой окружности и...
1 - Среди этих чисел найдите наименьшее общее кратное чисел 3 и 12....
3 - Найдите радиус кривизны траектории движения электрона влетевшего...
3 - ЗАДАНИЯ 1) Как вы думаете, на чем основывалась вера в торжество...
1 - Определи правильное и неправильное утверждения. Из плена джунгар...
2 - 3. Какой прием использован в строчках: «князь» — «раб»; «послал»...
3 - 1. Дерексіз сөзді табыңыз * А. Қалам B. Аула C. Бақыт D. Тақта 2....
1 - Подберите название широкой темы, в составе которой могут бытьузкие...
3
(sinα + cosα)² = sin²α + 2sinα·cosα + cos²α = sin²α + cos²α + 2sinα·cosα =
Так как -3п < α < -2п, что равносильно -п < α < 0 (мы прибавили к обеим частям 2п, что равно периоду синуса и косинуса), то угол α ∈ нижней полуплоскости (III четверть + IV четверть), где знак синуса отрицателен. Поскольку sinα·cosα = 1/5 > 0, то sinα и cosα должны быть одного знака
⇒ α ∈ третьей четверти ⇒ sinα < 0, cosα < 0 ⇒ sinα + cosα < 0
ОТВЕТ: