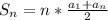Три числа, сумма которых равна 7, составляют возрастающую прогрессию. если бы большее из этих чисел было на 1 меньше, то числа бы составили арифметическую прог. сколько членов прогрессии надо взять, чтобы их сумма была равно 255?
Другие вопросы по теме Алгебра
Популярные вопросы
- Берілген сөздердің қайсысы негізгі етістік, қайсысы туынды етістік екендігін...
2 - Как скачать зумя его выкинула просто ...
3 - Закон должен быть строг, а люди снисходительны. Как вы понимаете? ...
1 - 3 задание Буду очень благодарен...
2 - здесь нужно найти стороны а и б я решила уже через 100 ну только осталось...
1 - 1)Как определить в каких ионах и веществах наблюдается насыщенность ковалентной...
3 - Гидрид бария массой 1,39 г внесли в 71,8 мл 16%-него раствора серной кислоты...
3 - Стр.60 зад.Р. С каким цветом ассоциируется у вас тот или иной герой повести?...
2 - Мәтінді мұқият оқы. «Ереже» сөзінің синонимдік қатарын анықта. Жол ережелерін...
3 - Unit 18 - Business. Phrasal verbs. 1. Vocabulary: find the matching phrasal...
3
(*) - формула для суммы арифметической прогрессии: