Три числа, из которых третье равно 9, образуют геометрическую прогрессию. Если вместо 9 взять 5, то эти числа составят арифметическую прогрессию. Найдите эти числа.

Ответы

помидор2324 24.12.2021 06:00

а) х = 1; у = 3

б) х = 25; у = 15

Объяснение:

Обозначим неизвестные числа соответственно

как х и у .

Известно, что последовательность

x; y; 9

является геометрической прогрессией, т.е.

любой член прогрессии вычисляется по формуле

$b_{n}=b_{1} \cdot q^{n-1} \\ \\ b_{n}= \sqrt{b_{n - 1} \cdot b_{n + 1}} \\ b_{2}= \sqrt{b_{1} \cdot b_{3}} \\ y = \sqrt{x\cdot9} = 3 \sqrt{x}$

а последовательность

x; y; 5

является арифметической прогрессией, т.е. любой член прогрессии вычисляется по формуле

$a_{n}=a_{1} + d \cdot({n-1}) \\ \\ a_{n} = \frac{a_{n - 1} +a_{n + 1} }{2} \\ a_{2} = \frac{a_{1} +a_{3} }{2} \\ y = \frac{x + 5}{2}$

Это значит, что имеем систему:

$\begin{cases}y = 3 \sqrt{x} \\ y = \dfrac{x + 5}{2} \end{cases} \\ \begin{cases}y = 3 \sqrt{x} \\ 3\sqrt{x} = \dfrac{x + 5}{2} \end{cases} \\ (6\sqrt{x} )^{2} = x^{2} + 10x + 25$

Очевидно, что х ≥0, следовательно

$36x = {x}^{2} + 10x + 25 \\ x^{2} - 26x + 25 = 0$

По Т. Виета:

$(x - 1)(x - 25) = 0 \\ x_{1} = 1 \\ x_{2} = 25$

Подставляем в систему

$\small\begin{cases} \left[ \begin{array}{l}x = 1 \\ x = 25 \end{array} \right. \\ y = 3 \sqrt{x} \end{cases}{ < }{=}{ } \left[ \begin{array}{l} \begin{cases}x = 1 \\ y = 3 \sqrt{x} \end{cases} \\ \begin{cases}x = 25 \\ y= 3 \sqrt{x} \end{cases} \end{array} \right. < = \left[ \begin{array}{l} \begin{cases}x = 1 \\ y = 3 \end{cases} \\ \begin{cases}x = 25 \\ y= 15 \end{cases} \end{array} \right.$

Получили 2 варианта значений для пары х и у:

а) х = 1; у = 3

И тогда прогрессии будут:

- геометрическая: 1; 3; 9

$b1 = 1;\: \: q = 3 \\$

- арифметическая 1; 3; 5

$a_1=1;\:\: d=2$

б) х = 25; у = 15

И тогда прогрессии будут:

- геометрическая: 25; 15; 9 убывающая прогрессия с

$b1 = 25;\: \: q = \frac{3}{5} \\$

- арифметическая 25; 15; 5 убывающая прогрессия с

$a_1=25;\:\: d= -10$

ПОКАЗАТЬ ОТВЕТЫ

SlavZgr 24.12.2021 06:00

Объяснение:

Пусть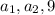 a_1,a_2,9 геометрическая прогрессия

По условию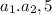 a_1.a_2,5 образуют арифметическую прогрессию

По характеристическим свойствам геометрической и

арифметической прогрессии имеем, что

$a_2^2=9a_1~~\rightarrow ~~a_1=\dfrac{a_2^2}{9} a_1+5=2a_2~~\rightarrow ~~2a_2-a_1=52a_2-\dfrac{a_2^2}{9}=5;~~18a_2-a_2^2=45;~~a_2^2-18a_2+45=0po~Vieta1)~a_2=15;~a_1=\dfrac{15^2}{9} =252)~a_2=3;~a_1=\dfrac{3^2}{9} =1$