1. Алгебра
  2. только распишите чтобы было понятно

только распишите чтобы было понятно

tatgomer tatgomer    2   05.08.2022 01:16    1

Ответы
Tittans7 Tittans7  05.08.2022 01:16

1) (0; 5) ;

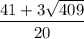2) ( 4; \dfrac{41+3\sqrt{409} }{20})

3)  [ - 3; - 1) ∪ ( -1; 4]

Объяснение:

Решить неравенства

1) 0,75 ^{6x^{2} -30x } 1 \Leftrightarrow0,75 ^{6x^{2} -30x } 0,75 ^{0}

Так как основание степени 0<0,75 <1 , то  показательная функция  y= 0,75^{t}убывающая.

Тогда получим

6x^{2} -30x < 0|:6\\x^{2} -5x < 0;\\x(x-5) < 0;\\x(x-5)=0;\\x{_1}=0;x{_2}= 5

Определим знак ( во вложении) и получим

0 < x < 5, то есть х ∈ (0; 5).

ответ : 0 < x < 5

2) \log {_\sqrt{5} }(5+0,1x) \log {_\sqrt{5} }(x) +\log {_\sqrt{5} }(x-4)

Так как логарифм определен на множестве положительных чисел, то найдем ОДЗ неравенства

\left \{\begin{array}{l} 5+0,1x 0, \\ x 0,\\ x - 4 0;\end{array} \right.\Leftrightarrow \left \{\begin{array}{l} 50+x 0, \\ x 0,\\ x 4;\end{array} \right.\Leftrightarrow\left \{\begin{array}{l} x -50, \\ x 0,\\ x 4;\end{array} \right.\Leftrightarrow x 4.

\log {_\sqrt{5} }(5+0,1x) \log {_\sqrt{5} }(x(x-4));

\log {_\sqrt{5} }(5+0,1x) \log {_\sqrt{5} }(x^{2} -4x)

Так как \sqrt{5} 1, то логарифмическая функция y=\log{_\sqrt{5} }tвозрастающая .

5+0,1x x^{2} -4x;\\5+0,1x-x^{2} +4x 0;\\-x^{2} +4,1x+5 0|\cdot (-10);\\10x^{2} -41x-50 < 0

10x^{2} -41x-50=0;\\D= (-41) ^{2} -4\cdot10\cdot(-50)=1681+2000=3681 0

\sqrt{D} =\sqrt{9\cdot 409 } =3\sqrt{409}

x{_1}= \dfrac{41-3\sqrt{409} }{20} ;x{_2}= \dfrac{41+3\sqrt{409} }{20}

Определим знак ( во вложении)

Тогда

\dfrac{41-3\sqrt{409} }{20} < x < \dfrac{41+3\sqrt{409} }{20}

Учтем ОДЗ и получим

Так как \dfrac{41+3\sqrt{409} }{20}\approx5,1, то   4 < x < \dfrac{41+3\sqrt{409} }{20}

ответ: 4 < x < \dfrac{41+3\sqrt{409} }{20}

3) \dfrac{x^{2} -x-12}{(x+1) ^{2} } \leq 0

Разложим числитель на множители. Для этого решим квадратное уравнение

x^{2} -x-12=0;\\D=(-1)^{2} -4\cdot1\cdot(-12)= 1+48=49=7^{2} ;x{_1}=\dfrac{1-7}{2} =-\dfrac{6}{2} =-3;x{_2}=\dfrac{1+7}{2} =\dfrac{8}{2} =4.

x^{2} -x-12=(x-4)(x+3)

Тогда неравенство принимает вид:

\dfrac{(x-4)(x+3)}{(x+1) ^{2} } \leq 0

Решим неравенство методом интервалов .

x=4;x=-3;\\x\neq -1

Определим знак ( во вложении)

Тогда получим  

х ∈ [ - 3; - 1) ∪ ( -1; 4]


только распишите чтобы было понятно
только распишите чтобы было понятно
только распишите чтобы было понятно
только распишите чтобы было понятно
ПОКАЗАТЬ ОТВЕТЫ
ojitovtitan ojitovtitan  05.08.2022 01:16

Відповідь:

Пояснення:


только распишите чтобы было понятно
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Ьрнрг Ьрнрг  19.11.2019 14:59
Первое здание а б нужно, заранее...
Nastya3748 Nastya3748  19.11.2019 15:08
Заполнить таблицу и построить график функции y=2x-1 ​...
maksderbenevMarc maksderbenevMarc  19.11.2019 15:08
Хелпуйте народ! кому не сложно решите...
Скотч7Рулит Скотч7Рулит  19.11.2019 15:09
Постройте график функции вычислить координаты точек пересечения y=1 5/6x -2.2​...
coollkid coollkid  17.05.2020 19:47
Принадлежат ли графику уравнения 5х-3у=15 точка А(0;0) ;В(0;-5) ; С(3;0) ....
DenisBru4anovvv DenisBru4anovvv  17.05.2020 19:46
Решите квадратное уравнение: 4x2-28x + 24 = 0...
rahimzhan20p0dqkg rahimzhan20p0dqkg  17.05.2020 19:46
МОЛЮ с 5 заданием(первое сверху)....
Mila2019 Mila2019  17.05.2020 19:46
Не используя формулу корней, найди корни квадратного уравнения x2 + 24x + 128 = 0. (Корни запиши в порядке убывания)...
youngfng youngfng  17.05.2020 19:46
Ради бога очень важно с системой неравенств:...
Yanas7 Yanas7  17.05.2020 19:46
Постройте треугольник по сторонам AB=5 см, ВС=7 см и углу ∠АВС = 50о. В полученном треугольнике постройте серединный перпендикуляр к стороне АС...

Популярные вопросы