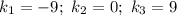Только можно подробное объяснение!
Задание:
Постройте график функций. Определите при каких значениях k прямая y=kx не имеет с графиком общих точек.
Другие вопросы по теме Алгебра
Популярные вопросы
- Prepare at home. choose the animal you would like to talk to....
1 - Выполните по действиям (4 1/2-3 4/10: 1 2/15) + 1/6 + 5...
2 - Напишите 8 вершин гор, горы на которых находятся эти вершины...
3 - Запишите предложения. выпишите из них сказуемые, определите...
3 - Зо дало мені вивчення середньовічньой літератури?...
2 - Сообщение на тему татарские театры республики башкортостан...
2 - Какое значение имело проходящая через село дорога для крестьянских...
2 - Вычислите значение выражения рациональным...
1 - ответ вопрос бел лит нямоглы бацька 1-10 вопросов...
2 - Питну соду маса якої становила 25.2г прожарили а її твердий...
3
Область определения функции:
Применим свойство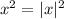 и получаем следующее:
и получаем следующее:
Следовательно, изобразим график функции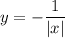 с учетом области определения (см. вложение).
с учетом области определения (см. вложение).
Прямая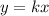 — прямая пропорциональность — не будет иметь с графиком функции
— прямая пропорциональность — не будет иметь с графиком функции 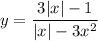 ни одной общей точки (см. вложение), если:
ни одной общей точки (см. вложение), если:
ответ: