Точки максимума и минимума
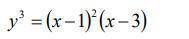
Другие вопросы по теме Алгебра
Популярные вопросы
- Вкаком слове (или каких словах) действует закон обязательного оглушения...
3 - Укажите одного (надо указать троих) деятеля - вашего земляка ( жизнь...
3 - Сапоги стоили 30 000тг.цена на них последовательно пониждалась 2...
3 - Всумме возраст кати, её мамы и бабушки составляет 124 года. известно,...
3 - Перескажите текст ученый и изобретатель, основоположник теоретической...
1 - Средняя калорийность листьев - 100 ккал на 100 г. сцинк питается...
3 - Подбирите и запишите 8,10слов с орфограммой проверяемые согласные...
2 - Найдите элемент в составе гидрида в котором массовая доля водорода...
1 - Свитер стоит 8000тг.цена на него последовательно повышалась 2раза...
2 - Перечислите: 1) 10 активных металлов. 2) все щёлочи. 3) все щелочные,...
1
Объяснение:
y^3=(x-1)^2 *(x-3), y=корень кубический из (x^2-2x+1)(x-3)= (корень кубический обозначу V), y=V(x^3-3x^2-2x^2+6x+x-3)=
V(x^3 -5x^2 +7x -3) (^ - значок степени), y=(x^3 -5x^2 +7x -3)^ 1/3
берем производную по формуле x^n=n*x^(n-1),, но это сложная функция.
y'=1/3 *(x^3-5x^2+7x-3)^ (-2/3) *(3x^2-10x+7)=(3x^2-10x+7)/3(x^3-5x^2+7x_3)^ 2/3 =(3x^2-10x+7)/корень кубический и под корнем (x^3-5x^2+7x-3)^2,
y'=0 когда числитель = 0, 3x^2-10x+7=0, x1=1, x2=7/3 -критические точки
+ + + + + +[1] - - - - - - - - [7/3] + + + + + + , 1-точка max, 7/3 -точка min