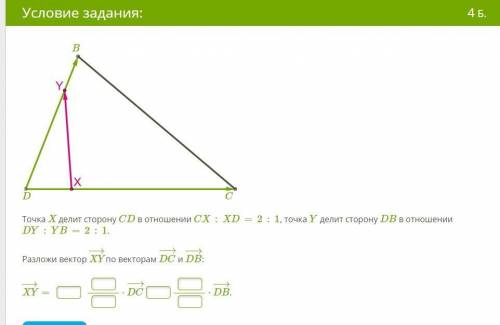
Точка X делит сторону CD в отношении CX:XD=2:1, точка Y делит сторону DB в отношении DY:YB=2:1. Разложи вектор XY−→ по векторам DC−→− и DB−→−: XY−→=⋅DC−→−⋅DB−→−.
Другие вопросы по теме Алгебра
Популярные вопросы
- Найди значение выражения 54-29...
1 - 2. Перечислите не менее 5 словарей,дайте грамотное описание (название, автор,...
3 - Батырлар киетин сауыт калай аталадыыы?...
2 - Task. Part 1 Complete the sentences according to text.1. Long distant communicationIavailable...
1 - Пацаны халява по раздаю бесплатно. Как вам такое?...
1 - Не выполняя арифметические действия покажите что сумма чисел 63+161 делится на...
3 - ЗАМЕТКА В ШК.ГАЗЕТУ ТРАДИЦИИ КАЗАХСКОЙ СЕМЬИ И ОТМЕЧУ КАК ЛУЧШИЙ...
3 - 20 Read and write. (See Student s Book page 32.) Ask and say. AnimalHow manyWhere...
1 - Отметь на карте территории карлуков Тимаков огузов...
1 - Көмектесіндерш соңғы калды...
1
Сначала найдем координаты точек X и Y.
Так как точка X делит сторону CD в отношении CX:XD=2:1, то координаты X можно найти как:
X = (1/3)*C + (2/3)*D
Аналогично, координаты точки Y можно найти как:
Y = (2/3)*D + (1/3)*B
Теперь найдем вектор XY→:
XY→ = Y - X
= ((2/3)*D + (1/3)*B) - ((1/3)*C + (2/3)*D)
= (1/3)*B - (1/3)*C
Теперь разложим вектор XY→ по векторам DC→− и DB→−.
Разложение вектора XY→ по вектору DC→−:
Для этого нужно найти проекцию вектора XY→ на вектор DC→−. Формула для проекции вектора a на вектор b:
proj_b(a) = (a * b) / |b|
Где a * b - скалярное произведение векторов a и b, и |b| - длина вектора b.
В данном случае имеем:
a = XY→ = (1/3)*B - (1/3)*C
b = DC→− = C - D
Теперь вычислим проекцию:
proj_DC-→ (XY→) = ((1/3)*B - (1/3)*C * (C - D)) / |C - D|
Поскольку вектор DC−→− направлен от точки C к точке D, его длина равна:
|C - D| = sqrt((Dx - Cx)^2 + (Dy - Cy)^2)
Теперь можно вычислить проекцию:
proj_DC-→ (XY→) = ((1/3)*Bx - (1/3)*Cx) * (Dx - Cx) + ((1/3)*By - (1/3)*Cy) * (Dy - Cy) / sqrt((Dx - Cx)^2 + (Dy - Cy)^2)
Аналогично, для разложения вектора XY→ по вектору DB→−, найдем проекцию вектора XY→ на вектор DB→−:
proj_DB-→ (XY→) = ((1/3)*Cx - (1/3)*Bx) * (Bx - Dx) + ((1/3)*Cy - (1/3)*By) * (By - Dy) / sqrt((Bx - Dx)^2 + (By - Dy)^2)
Итак, мы разложили вектор XY→ по векторам DC→− и DB→−. Полученные формулы для проекций можно вычислить, подставив известные координаты точек C, D и B.