1. Алгебра
  2. Tg2x = 9sin^2x +4sinxcosx

Tg2x = 9sin^2x +4sinxcosx -3cos^2x решите уравнение

doggster doggster    3   27.09.2019 01:00    2

Ответы
khabarovanastya khabarovanastya  08.10.2020 21:31

По формуле понижения степени и синусу двойного угла:

tg2x=9\cdot\dfrac{1-\cos 2x}{2} +2\sin 2x-3\cdot\dfrac{1+\cos 2x}{2} \\ \\ tg2x=\dfrac{9-9\cos 2x-3-3\cos 2x}{2}+2\sin 2x\\ \\ tg2x=3-6\cos 2x+2\sin 2x

Умножим левую и правую части уравнения на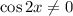 \cos 2x\ne 0, получим:

\sin 2x=3\cos 2x-6\cos^22x+2\sin 2x\cos 2x\\ \sin 2x-3\cos 2x+6\cos^22x-2\sin 2x\cos 2x=0\\ (\sin 2x-3\cos 2x)-2\cos 2x(\sin 2x-3\cos 2x)=0\\ (\sin 2x-3\cos 2x)(1-2\cos 2x)=0


Произведение равно нулю, если хотя бы один из множителей обращается в нуль.

\sin 2x-3\cos 2x=0~|:\cos 2x\ne0\\ tg2x-3=0\\ 2x=arctg3+\pi n,n \in \mathbb{Z}\\ x=0.5actg3+0.5\pi n,n \in \mathbb{Z}


1-2\cos 2x=0\\ \cos 2x=0.5\\ 2x=\pm\frac{\pi}{3}+2\pi n,n \in \mathbb{Z}\\ x=\pm\frac{\pi}{6}+\pi n,n \in \mathbb{Z}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
dilnaramusaeva dilnaramusaeva  20.07.2019 17:20
:с решите уравнение: (4х-3)(2-х)=(-2+3)(3+2х)...
MrMut222 MrMut222  20.07.2019 17:20
Можно ли сократить уравнение 2y/y^2...
не0тличник не0тличник  20.07.2019 17:20
Cкількома можна вибрати 5 яблук із 12...
КАТЯ3105 КАТЯ3105  20.07.2019 17:20
При каких k корни уравнения x^2 - (3k+2)*x + k^2 удовлетворяют соотношению x1 = 9x2...
homka16072006 homka16072006  20.07.2019 17:20
Нужно к углам от 0° до 90°: 1) sin 152° 2)cos124° 3)sin242° 4)cos196° 5)sin175° 6)cos 235° 7)tg 111° 8) ctg 215° 9)sin 312° 10) cos 166° 11)sin 290° 12)ctg 163° 13) tg 286°...
Snicerenko1980 Snicerenko1980  20.07.2019 17:20
Заранее огромнейшее ! : ) нужно возвести в квадрат: а) а^2-6ав+9в б) 16а^2+8ав+в^2 в)4/9а^2-2ав+9/4в^2 г)1/4а^2-ав+в^2 д)1-2ав+а^2в^2 е)а^4+2а^2в+в^2...
ВладИК08123 ВладИК08123  20.07.2019 17:20
Как представить в виде произведения...
KsehiaKomleva KsehiaKomleva  20.07.2019 17:20
Куглам от 0° до 90°: 1) sin 152° 2)cos124° 3)sin242° 4)cos196° 5)sin175° 6)cos 235° 7)tg 111° 8) ctg 215° 9)sin 312° 10) cos 166° 11)sin 290° 12)ctg 163° 13) tg 286° 14)cos...
gdhdf gdhdf  20.07.2019 17:20
умоляю ! вы нужны мне снова по-моему нужно представить в виде многочлена: а) (х-6)^2 б) (4а+1)^2 в) (5а+8) г) (-3в+а)^2 д) (а^2-7)^2 е) (-2м-9п)^2 заранее огромное вы выручаете...
Gamonga Gamonga  20.07.2019 17:20
Возведите в куб выражение -2a(в 20 степени) *с (в 12 степени )*x...

Популярные вопросы