 - найдите производную,
- найдите производную,
Другие вопросы по теме Алгебра
Популярные вопросы
- Буду : ) составьте 15 предложений на тему : i don t like...
3 - Люди найти ошибки и зделать решение правильна 19: 2=9(астача 1) 20: 6=3(астача1)...
3 - Вычислите объем и площадь поверхности куба с ребром 4 дм...
3 - Моторная лодка км по течению реки и 12 км против течения реки,затратив на...
2 - Мальчик принесёт синицу домой в какой форме стоит глагол принесёт...
3 - Использование гидрокарбаната натрия...
3 - Подскажите, , аргументы из произведений к сочинению по языку на тему не...
3 - Как правильнее на суше или на суши?...
3 - Написать правильно дано си и решение а)сколько тела 7,2 км/ч .выразите эту...
1 - Напиши краткие ответы на эти вопросы о твоей классной комнате. язык. рабочая...
3
Объяснение: f'(х) = 3/2√х-15
По формуле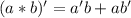
избавимся от иррациональности
теперь подставим
и не забываем про 15х, получится конечный ответ