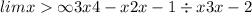
Другие вопросы по теме Алгебра
Популярные вопросы
- 2 часть: Wir haben Kühe Hühner und natürlich unser Vento. Ja und Schafe,...
1 - Господа астрономы! Можно ли наблюдать ПОЛНОЕ солнечное затмение на Луне...
3 - В каком ряду (рядах) во всех словосочетаниях связь примыкание? а) ее заботит,...
3 - Орфографический разбор частицы не. ответьте а то в учебнике написано и я...
1 - Через вершину B прямого кута трикутника ABC проходить пряма, перпендикулярна...
1 - Запишите десятичную дробь в виде смешанного числа и сократить его дробнвю...
2 - описание последней встречи Герасима и гаврилы в рассказе Муму перед тем...
2 - They looknice, beautiful, big, new, old,fresh,clean, funny,great, long,...
3 - Яка з названих річок належить до гірсько-рівниннх: Південний Буг;Дністер;Дніпро;Черемош....
3 - Найдите 24% от проверьте вот так ...
3
ответ: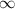
Мы знаем если - некоторое число, то
- некоторое число, то 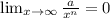 , где
, где 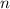 - натуральное число
- натуральное число
Получим: