$\left \{ {(x+6y)^2=7y} \atop {(x+6y)^2=7x}} \right.$ $\left \{ {{(7x-2y)^2=25y} \atop {(2x-7y)^2=25y}} \right.$ $\left \{ {{(x-2)(y+3)=0} \atop {(x^2-4)(y+4)=3x}} \right.$ $\left \{ {{(3x-8y)^2=-5x} \atop {(3x-8y)^2=-5y}} \right.$ $\left \{ {{(x-3)(y-7)=0} \atop {(x^2-9)(y-4)=24x}} \right.$ решить системы уравнения. 50 !

Ответы

luda12349 10.10.2020 01:13

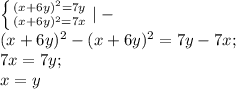1. $\left \{ {{(x+6y)^2=7y} \atop {(x+6y)^2}=7x} \right.|-\\ (x+6y)^2-(x+6y)^2=7y-7x;\\7x=7y;\\x=y$ Уравнение прямой, которая наклонена на 45°.

2.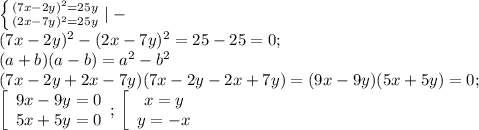 $\left \{ {{(7x-2y)^2=25y} \atop {(2x-7y)^2=25y}} \right.|-\\ (7x-2y)^2-(2x-7y)^2=25-25=0;\\(a+b)(a-b)=a^2-b^2\\(7x-2y+2x-7y)(7x-2y-2x+7y)=(9x-9y)(5x+5y)=0;\\\left[\begin{array}{ccc}9x-9y=0\\5x+5y=0\\\end{array};\\\left[\begin{array}{ccc}x=y\\y= -x\\\end{array}$ Это две прямые которые наклонены на 45° и 135°.

3.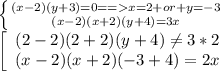 $\left \{ {{(x-2)(y+3)=0==x=2+or+y=-3} \atop {(x-2)(x+2)(y+4)=3x}} \right. \\\left[\begin{array}{ccc}(2-2)(2+2)(y+4)\neq 3*2\\(x-2)(x+2)(-3+4)=2x\\\end{array}$ Мы выяснили, что х≠2 т.к. второе уравнение не верно. Теперь узнаем какие значения х, при у=-3

$x^2-4-3x=0; D=9+16=5*5;\\x=\frac{3б5}{2}=4+and+(-1)$

Значит x={-1;4}

y= -3

4.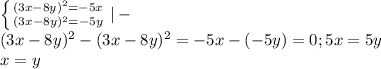 $\left \{ {{(3x-8y)^2=-5x} \atop {(3x-8y)^2=-5y} \right. |-\\(3x-8y)^2-(3x-8y)^2=-5x-(-5y)=0; 5x=5y\\x=y$ это уравнение прямой, которая наклонена на 45°

5. $\left \{ {{(x-3)(y-7)=0 == x=3+or+y=7} \atop {(x^2-9)(y-4)=24x}}\\\left[\begin{array}{ccc}(9-9)(y-4)\neq 24*3\\(x^2-9)(7-4<img src=$ )=24x\\\end{array};" alt="x^2-9=\frac{24x}{3}; x^2-9-8x=0; D=64+36=10*10\\ x=\frac{8б10}{2}=9+or+(-1 )" />)=24x\\\end{array};" /> x≠3 т.к. не выполняется второе уравнение, рассмотрим случаи, когда у=7