Другие вопросы по теме Алгебра
Популярные вопросы
- Высота треугольника делит ра 6 см и 15см в длину. вычислите область треугольника,если...
3 - Срешением два одинаковых металлических шарика 2нкл и -6нкл.какой заряд окажется...
2 - Из суммы 10 слагаемых каждое из которых равно 10 вычти 10....
1 - Какие памятники отрожают себе исламскую религию превидите примееры...
3 - Квадратный трёхчлен -2х^2+12х-18=0 |*(-1) 2(х^2-6х+9)=0 д=(-6)^2-4*9=0 найти...
1 - Из суммы 5 слагаемых каждое из которых равно 5 вычти 5...
1 - Найти область определения, множество значений и обратную ф-ию для данной:...
3 - Доведіть що чотирикутник abcd з вершинами а(-1; 5) b(4; 6) c(3; 1) d(-2; 0)...
3 - Списать предложения, определить виды сказуемых: 1.сейте разумное,доброе,вечное....
3 - ответить своими словами на следующий вопрос: почему так важно ясно представлять...
3
По теореме Виета :
или √x =1 , а √y = 4 и тогда x = 1 , а y = 16
или √x = 4 , а √y = 1 и тогда x = 16 , а y = 1
ответ : (1 ; 16) , (16 ; 1)
ОДЗ:
Сделаем замены . Получим систему:
. Получим систему:
Пользуясь обратной теоремой Виета, составим квадратное уравнение:
Следовательно:
Вернёмся к исходным переменным. Сначала разберём первый случай с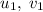 :
:
Второй вариант, очевидно, будет симметричен (получится перестановкой переменных):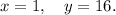
ответ: (1; 16) и (16; 1).