
решите систему уравнений
Другие вопросы по теме Алгебра
Популярные вопросы
- вологість повітря в кімнаті за температури 20 градусів цельсія становить 6г/м³....
2 - Побудуйте графік функції y=x⅓. За до графіка знайдіть значення функції, що відповідає...
1 - Найди: 1/6 Числа 78 а) 6 б) 1 % числа 600 в) 1/5 От 85 кг у меня завтра самостоятельная...
2 - Корень из 2, кто найдёт, тому буду подкидывать халявные...
2 - с литературой ) Объясните жанры романа «Мастер и Маргарита» такие как 1) Бытовой...
1 - 3. Позначте та підпишіть міста з кількістю населення понад 1 млн жителів....
2 - Задание № 1. Прочитай. Найди ошибки. Запиши текст в тетрадь правильно. Улов. В...
2 - Решите подробно 2ой вариант...
3 - Чому роман має назву Кава з кардамоном...
3 - Глобальные проблемы современности и пути их решения сочинение...
3
1) Работаем с первым уравнением.
Замена:
Замена:
2) Работаем со вторым уравнением.
Если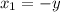 , то можно найти
, то можно найти 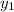 .
.
Если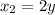 , то можно найти
, то можно найти 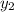 .
.
При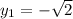 =>
=> 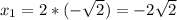
При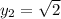 =>
=> 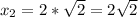
ответ: (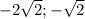 );
);
(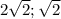 )
)