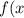$f(x)=\left \{ {{0}, x< 0 \atop ae^{-x}, x\geq0 }} \right.$
a = -1, b=2.

необходимо найти:

1. значение постоянной а, при котором f(x) будет плотностью распределения некоторой случайной величины х

2. интегральную функцию распределения f(x) этой случайной величины х.

3. мат. ожидание, дисперсию, среднее квадрат. отклонение.

4. вероятность попадания св ч в интервал (а,b).

построить графики функций f(x) и f(x)

Ответы

funny43 17.08.2020 15:50

Воспользовавшись одним из свойств плотности распределения

$\displaystyle \int\limits^{+\infty}_{-\infty} f(x)dx=1\\ \\ \\ \int\limits^{+\infty}_{-\infty}Ae^{-x}dx=\int\limits^{+\infty}_{0}Ae^{-x}dx=-Ae^{-x}\bigg|^{+\infty}_{0}=-A(0-1)=1~~\Rightarrow~~~\boxed{A=1}$

Заметим, что это показательное распределение с параметром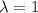 $\lambda =1$

$F(x)=\displaystyle \int\limits^{x}_{0}f(t)dt=\int\limits^{x}_{0}e^{-t}dt=-e^{-t}\bigg|^x_0=1-e^{-x},~~~ x\geq 0$

3) Математическое ожидание случ. величины X: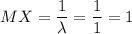 $MX=\dfrac{1}{\lambda}=\dfrac{1}{1}=1$

Дисперсия случ. величины X: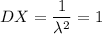 $DX=\dfrac{1}{\lambda^2}=1$

Среднее квадратическое отклонение: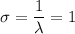 $\sigma =\dfrac{1}{\lambda}=1$

4) Вероятность того, что СВ Х попадет в интервал (-1;2), равна

P(-1

a = -1, b=2.необходимо найти:" />
<img src=

a = -1, b=2.необходимо найти:" />

ПОКАЗАТЬ ОТВЕТЫ

Tanyams 17.08.2020 15:50

Решение на фотографиях. Приятно удивлен увидеть здесь университетскую жизнь (теорвер). Если что, как берется неопределенный интеграл от xe^-x или x^2 * e^-x опущено, т.к. это легко делается с интегрирования по частям (в первом случае применяем единожды, во втором два раза). Графики можно начертить здесь www.desmos.com/calculator