Теория вероятности функция ф(х)
Задание #6
Другие вопросы по теме Алгебра
Популярные вопросы
- Найти поверхность и объем прямоугольного параллелепипеда если его...
2 - Произведение чисел 753 и 202 прибавить произведение чисел 404 и 909...
3 - Влевом колене сообрающихся сосудов есть ртуть, в правом вода.высота...
3 - Шить,пить,юла(буквы,звуки анализы сделать)...
1 - Проверочные слова к словам , пошел , плащадке , вернусь...
1 - За сутки 16 автомобилей выбросили в атмосферу 320 кг выхлопных газов....
1 - Выполни деление 268.00: 84,121.000: 11,196.196: 14,144.144: 12...
2 - Найти произведения первых трёх и последних трёх элементов массива...
2 - Всаду росло со кустов смородины осенью посадили еще 5 рядов по 10...
3 - Вшколу . спортинвентарь. в 3 клробках лежало 45 скалок поровну в...
2
а) Чтобы φ(x) была плотностью нужно:
Найдем интеграл: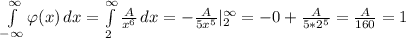
Отсюда А=160
б) Функция распределения есть:
При x≤2: F(x)=0
При x>2: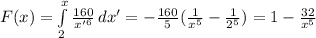
в) Искомая вероятность:
г) Мат. ожидание:
Дисперсия: