Теорема виета
сократи дробь (x+8) : x^2+22x+112 (x вводи в раскладке)

Если дискриминантом пользоваться нельзя, а только лишь теоремой Виета, то решение примерно таково.

Простым перебором возможных корней, которые должны быть делителями 112, найдём первый корень . Тогда второй корень находится из уравнения:

Разложение на множители приведённого квадратного уравнения имеет вид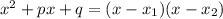 . В нашем случае:

Теперь можем сократить дробь:

ответ: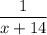 (при 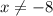).