Такой вопрос: как определить координаты точки на окружности, к примеру (x - 3)² + (y - 1)² = 1, такие, что отношение y/x - максимально?

Ответы

romka199811p0bu18 10.10.2020 22:29

Введем систему координат. Если окружность находится одновременно в 1 и 3 или 2 и 4 координатных плоскостях, то это отношение можно сделать сколь угодно большим (т.к. существует точка с абсциссой 0).

Пусть это не так. Тогда отношение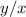 y/x - это тангенс угла наклона прямой, проходящей через начало координат и выбранную точку. Тангенс тем больше, чем ближе угол к 90°. Поэтому нужно найти угловой коэффициент касательной к верхней полуокружности. Технически сделать несложно: Проведем касательную, прямую из начала координат в центр. Получим два прямоугольных треугольника. Воспользовавшись формулой тангенса суммы, найдем искомой отношение. После упрощений: 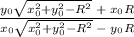$\frac{y_{0}\sqrt{x_{0}^{2}+y_{0}^{2}-R^{2}}\;+\;x_{0}R}{x_{0}\sqrt{x_{0}^{2}+y_{0}^{2}-R^{2}}\;-\;y_{0}R}$ ; Воспользовавшись формулой для окружности в примере ( 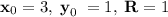$\textbf x_{0}=3,\;\textbf y_{0}\;=1,\;\textbf R=1$ ), получим, что максимальное отношение равно 0,75.