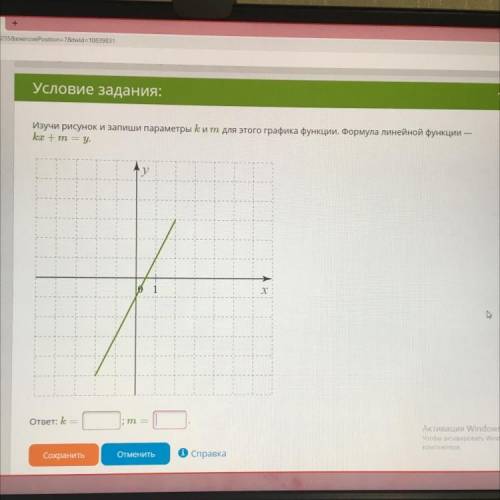
Tь. Изучи рисунок и запиши параметры k и т для этого графика функции. Формула линейной функции —
kx + m = y.

y=0,5x+0,5

Объяснение:

Чтобы заполнить таблицу параметров k и t для этого графика функции, нам нужно определить значения k и t, используя формулу линейной функции kx + m = y.

На рисунке указаны две точки: (4, 9) и (8, 15). Мы можем использовать эти точки, чтобы вычислить наклон (значение k) и свободный член (значение t) нашей функции.

1. Начнем с вычисления значения наклона k. Для этого используем формулу:

k = (y2 - y1) / (x2 - x1)

Где (x1, y1) и (x2, y2) - координаты двух точек. Давайте выберем первую точку (4, 9) и вторую точку (8, 15) для вычисления:

k = (15 - 9) / (8 - 4) = 6 / 4 = 1.5

Таким образом, значение наклона k для данного графика функции равно 1.5.

2. Теперь давайте вычислим значение свободного члена t. Для этого используем формулу:

t = y - kx

Мы можем использовать одну из точек, например, (4, 9), и подставить в формулу:

t = 9 - 1.5 * 4 = 9 - 6 = 3

Таким образом, значение свободного члена t для данного графика функции равно 3.

Итак, параметры k и t для данного графика функции равны: k = 1.5 и t = 3. Ваш ответ: k = 1.5, t = 3.