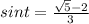Существуют ли значения t, при каждом их которых одновременно sint = (√5 - 2)/3? поясните ответ
Другие вопросы по теме Алгебра
Популярные вопросы
- Построй диаграмму показывающая количество мест, где растут мухоморы,...
1 - Маслозавод отправил 429кг масла в магазин.третью часть масла продали...
2 - Два автомобиля выехали из города одновременно в одном направлении.какое...
2 - Кто можэт быть глубочайшим? -кроме человека!...
3 - Решить с плотины выс. 2м. за 10 мин. падает 500 тонн воды. какая...
2 - Время мало , что если гипотенуза и острый угол одного прямоугольного...
2 - Впрямоугольном параллелепипеде ad=7 см, ab=корень из 18, угол...
2 - Сравните давление и силу давления: чем они различаются?...
1 - Найдите все углы образованные при пересечении двух параллельных...
1 - При восстановлении водородом смеси оксида железа (ii) и оксида...
2
sint = (√5 - 2)/3
число в правой части большее за -1 и меньшее за 1, значит учитывая периодичность функции sin и область ее значений да, существует бесконечное множество значений t, для которых