Суму n членів геометричної прогресії можна знайти за формулою Sn= 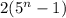
знайти а) S4. б)а5
Другие вопросы по теме Алгебра
Популярные вопросы
- Составьте 3 предложения с past simple, от них образовать отрицательные...
3 - С6 класс запасы угля хватает на 180 дней,если использорать 1/2 угля в...
1 - Решить рівняння в : (905 - 850) =5...
1 - Вкоробке 26 шариков 5 цветов белые, желтые, красные, синие, зелёные....
2 - Место произведеня зимнее утро в творчестве а.пушкина...
2 - Расставьте города-миллионеры в порядке их следования с запада на восток,...
1 - Кчему может засорение вентиляционной трубы?...
3 - Программа паскаль. составить программу, чтобы получились, как минимум...
3 - Держатели дисконтной карты книжного магазина получают при покупке скидку...
3 - Кданным прилагательные подобрать прилагательные - антонимы....
2
Объяснение:
ответ: S₄=1248 a₅=5000.