Сумма всех четных двузначных чисел разделилась на одно из них без остатка. Полученное частное отличается от делителя только порядком цифр, а сумма его цифр равна 9. Какое двузначное число являлось делителем? Сумма всех четных чисел 2430, тогда

Я решил и получил

И ещё

Получается ответ 45 не подходит т.к. не чётное число, так? Или я не правильно решил что-то.

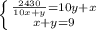
$\left \{ {{ \frac{2430}{10x + y} = 10y + x } \atop {x + y = 9}} \right.$
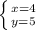
$\left \{ {{x = 4} \atop {y=5}} \right.$
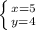
$\left \{ {{x=5} \atop {y=4}} \right.$

Ответы

Mellisa11111111 05.08.2021 12:10

У меня так же получилось , думаю что у нас правильно

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

Alihan184 29.09.2019 13:50

Укажите множество значений функции: y= cos 4x-5 1) [-4; 5] 2) [5; 5] 3) [-6; -4] 4) [-1; 9]...

oksanalap1 29.09.2019 13:50

Выражение а) 14с-4b+10b-4c б) 5*(2x-3)+10 в) 4*(x-5) -2*(x+3) г) c-(3c-(5c-1))...

ВаняАВЕР2006 29.09.2019 13:50

Найти значение выражения 4x-7y при x=7/12, y=-5/7...

лиана250 29.09.2019 13:50

Выражение (3a6d4)3⋅(6a3d3)0(27a3d3)2, где a≠0,d≠0....

Cool281 29.09.2019 13:50

Точка c - середина отрезка ab, точка d-середина bc . найдите ad ,если ab=36 см....

ichinichi 29.09.2019 13:50

Можете ? (уже второй раз решите уравнение: 2(х-+4)=х-10 ! )...

veronikasizonov 29.09.2019 13:50

Вмагазине работают два продавца-вася и сергей .каждый из них может быть занят с клиентом с вероятностью 0,4.при этом вероятность их одновременной занятости с клиентом-0,3.надите...

tattazhutdinov 29.09.2019 13:50

1. два автобуса отправились одновременно из одного села в другое растояние между сёлами 36 км. а первый автобус прибыл в назначеный пункт на 15 минут раньше второго...

marmeoladikp07wow 29.09.2019 13:50

Сократите дробь: x^2-27/x^2-5xy-3x+15y...

valentinateleg2607 29.09.2019 13:50

Пормогите: 1)решите уровнение 2(x-+4)=x-10 2)при каком значении а уравнение (а+4)х=а-3 не имеет корней?...

Популярные вопросы