Сумма коэффициентов второго и третьего слагаемых разложения ![\bigg(\sqrt[5]{x^2}-\dfrac{1}{2\sqrt[6]{x}}\bigg)^n](/tpl/images/4857/8603/240b5.png) равна
равна 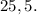 Написать член, не содержащий
Написать член, не содержащий 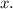
Другие вопросы по теме Алгебра
Популярные вопросы
- літій оксид масою 9 г розчинили у воді через утворений літій гідроксид пропустили...
3 - 3. Определите вероятность того, что при бросании кубика выпало числоочков, не...
2 - !Физика 1 курс Вариант-2 ...
3 - мне ? мне надо сегодня сдать... фото задач прикрепила...
2 - 3-тапсырма. «Су-тіршілік көзі» тақырыбында диалог құрастырыңдар. Тірек сөздерді...
2 - с тэстом Вопрос 1 Пока нет ответа : 1 Не отмеченоОтметить вопрос Текст вопроса...
2 - дай розгорнуту відповідь на запитання: яку роль відіграють гумор і сатира в...
3 - пусть это заметят професионалы 1.Каждая рамная пила в бревне пропиливает паз...
1 - To‘g‘ri to‘rtburchak shaklidagi bog‘ning perimetri 360 m. Dinoraning bir qadami...
3 - Guten Abend, Herr und Frau Schmidt! Wie geht es ... ? dirIhneneuchWie alt ......
3
Бином Ньютона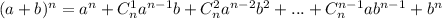 .
.
В задании![a=\sqrt[5]{x^2}=x^{\frac{2}{5}}\ ,\ \ b=-\dfrac{1}{2\sqrt[6]{x}}=-\dfrac{1}{2}\cdot x^{-\frac{1}{6}}](/tpl/images/4857/8603/b5277.png) .
.
Запишем разложение.
Сумма коэффициентов 2 и 3 слагаемых разложения равна
Показатель степени равен n=17 .
Член разложения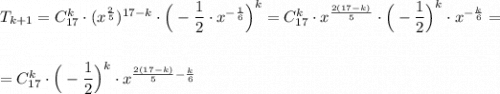
, который не содержит х , имеет показатель степени при х , равный нулю, поэтому
Тогда необходимый нам член разложения имеет номер k+1=13 ,