Сумма двух натуральных чисел равна 2021 а их наименьшее общее кратное равно 12040. Найдите наибольший общий делитель для этих двух чисел.

Ответы

Dima1911 15.10.2020 20:11

ответ: 43

Объяснение:

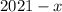Пусть одно из чисел равно , тогда второе 2021-x .

Пусть:

NOD(x;2021-x)=t

Тогда:

$x=at\\2021-x=bt\\at+bt=2021\\t(a+b) = 2021=43*47\\NOK(x;2021-x)=abt=12040=43*2^3*5*7\\\left \{ {{t(a+b)=43*47} \atop {abt=43*8*5*7}} \right.$

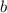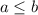Где и взаимнопростые натуральные числа. Для определенности будем считать, что $a\leq b$ .

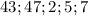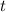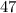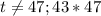Заметим, что числа 43 ; 47;2;5;7 простые. Из второго уравнения очевидно, что не делится на , то есть $t\neq 47;43*47$ .

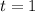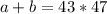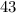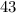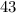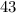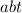Предположим теперь, что t=1 , тогда a+b=43*47 , но тогда, поскольку сумма двух чисел делится на , то либо каждое из них делится на , либо не одно из них не делится на . Если каждое из них делится на , то abt делится на 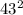43^2 , но правая часть второго равенства делится только на первую степень числа 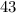. Если же оба из них не делятся на 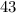, то с учетом того, что 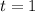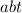t=1 , abt не делится на 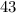. То есть мы пришли к противоречию.